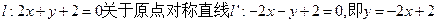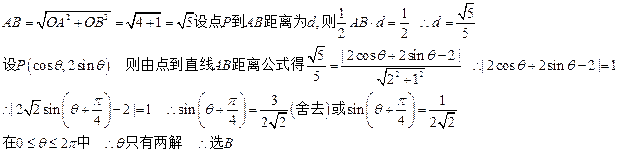题目内容
设直线l:2x+y+2=0关于原点对称的直线为l′.若l′与椭圆x2+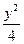
=1的交点为A、B，点P为椭圆上的动点，则使△PAB的面积为
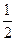的点P的个数为（ ）
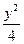=1的交点为A、B，点P为椭圆上的动点，则使△PAB的面积为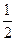的点P的个数为（ ）| A．1 | B．2 | C．3 | D．4 |
B
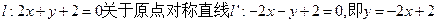
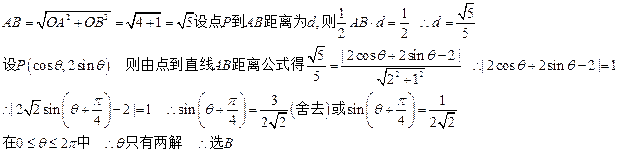
练习册系列答案
相关题目
题目内容
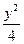=1的交点为A、B，点P为椭圆上的动点，则使△PAB的面积为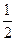的点P的个数为（ ）| A．1 | B．2 | C．3 | D．4 |
；（1）由曲线C上任一点E向X轴作垂线，垂足为F，
。问：点P的轨迹可能是圆吗？请说明理由；（2）如果直线L的斜率为
，且过点
，直线L交曲线C于A，B两点，又
，求曲线C的方程。 
中的抛物线
的焦点
作一条倾斜角为
的直线与抛物线相交于A，B两点。
表示A，B之间的距离；
的大小是与
，直线
：
，
为平面上的动点，过点
，且
．
的方程；
过定点
，圆心
轴交于
、
两点，设
，
，求
的最大值．
过点P(0,2), 且在
轴上截得的弦RG的长为4.
(０，１)，作轨迹
的两条互相垂直的弦
、
，设
、
，试判断直线
是否过定点？并说明理由．
轴上，它的一个顶点恰好是抛物线
的焦点，离心率
，过椭圆的右焦点
作与坐标轴不垂直的直线
交椭圆于
两点．
是线段
上的一个动点，且
，求
的取值范围；
是点
关于
，使得
三点共线？若存在，求出定点
的两个顶点分别
的坐标为
，
，平面内两点
同时满足下列条件：
；②
；③
∥
的轨迹方程；
的直线
与（1）中轨迹交于
两点，求
的取值范围
,则M等于( )
