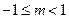题目内容
设动点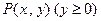 到定点
到定点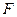
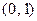 的距离比它到
的距离比它到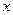 轴的距离大1,记点
轴的距离大1,记点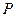 的轨迹为曲线
的轨迹为曲线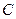 .
.
(1)求点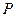 的轨迹方程;
的轨迹方程;
(2)设圆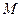 过
过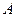
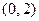 ,且圆心
,且圆心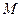 在曲线
在曲线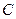 上,
上,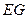 是圆
是圆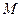 在
在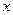 轴上截得的弦,试探究当
轴上截得的弦,试探究当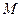 运动时,弦长
运动时,弦长 是否为定值?为什么?
是否为定值?为什么?
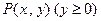 到定点
到定点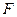
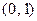 的距离比它到
的距离比它到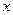 轴的距离大1,记点
轴的距离大1,记点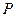 的轨迹为曲线
的轨迹为曲线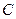 .
.(1)求点
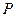 的轨迹方程;
的轨迹方程;(2)设圆
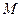 过
过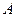
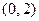 ,且圆心
,且圆心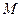 在曲线
在曲线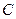 上,
上,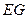 是圆
是圆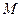 在
在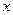 轴上截得的弦,试探究当
轴上截得的弦,试探究当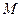 运动时,弦长
运动时,弦长 是否为定值?为什么?
是否为定值?为什么?(1)曲线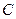 方程是
方程是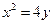
(2)当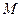 运动时,弦长
运动时,弦长 为定值4
为定值4
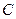 方程是
方程是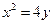
(2)当
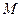 运动时,弦长
运动时,弦长 为定值4
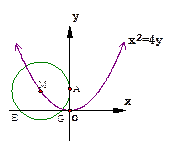
为定值4(1)依题意知,动点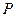 到定点
到定点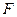
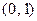 的距离等于
的距离等于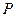 到直线
到直线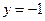 的距离,曲线
的距离,曲线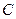 是以原点为顶点,
是以原点为顶点,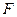
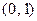 为焦点的抛物线………………………………2分
为焦点的抛物线………………………………2分
 ∵
∵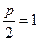 ∴
∴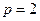
∴ 曲线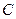 方程是
方程是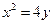 ………4分
………4分
(2)设圆的圆心为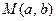 ,∵圆
,∵圆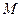 过
过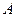
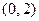 ,
,
∴圆的方程为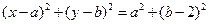 ……………………………7分
……………………………7分
令 得:
得: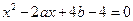
设圆与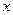 轴的两交点分别为
轴的两交点分别为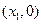 ,
,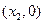
方法1:不妨设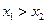
 ,由求根公式得
,由求根公式得
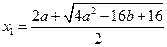 ,
, …………………………10分
…………………………10分
∴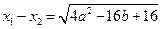
又∵点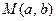 在抛物线
在抛物线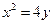 上,∴
上,∴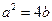 ,
,
∴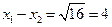 ,即
,即 =4--------------------------------------------------------13分
=4--------------------------------------------------------13分
∴当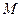 运动时,弦长
运动时,弦长 为定值4…………………………………………………14分
为定值4…………………………………………………14分
〔方法2:∵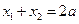 ,
,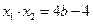
∴
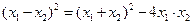
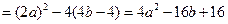
又∵点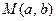 在抛物线
在抛物线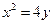 上,∴
上,∴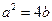 ,∴
,∴ 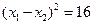
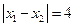
∴当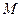 运动时,弦长
运动时,弦长 为定值4〕
为定值4〕
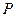 到定点
到定点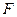
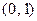 的距离等于
的距离等于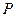 到直线
到直线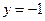 的距离,曲线
的距离,曲线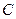 是以原点为顶点,
是以原点为顶点,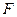
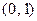 为焦点的抛物线………………………………2分
为焦点的抛物线………………………………2分 ∵
∵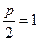 ∴
∴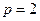
∴ 曲线
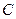 方程是
方程是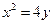 ………4分
………4分(2)设圆的圆心为
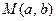 ,∵圆
,∵圆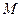 过
过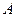
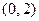 ,
,∴圆的方程为
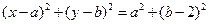 ……………………………7分
……………………………7分令
 得:
得: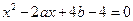
设圆与
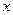 轴的两交点分别为
轴的两交点分别为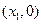 ,
,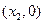
方法1:不妨设
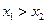
 ,由求根公式得
,由求根公式得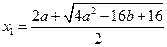 ,
, …………………………10分
…………………………10分∴
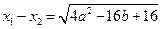
又∵点
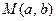 在抛物线
在抛物线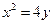 上,∴
上,∴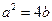 ,
,∴
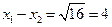 ,即
,即 =4--------------------------------------------------------13分
=4--------------------------------------------------------13分∴当
 运动时,弦长
运动时,弦长 为定值4…………………………………………………14分
为定值4…………………………………………………14分〔方法2:∵
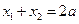 ,
,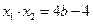
∴

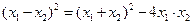
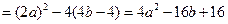
又∵点
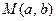 在抛物线
在抛物线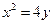 上,∴
上,∴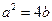 ,∴
,∴ 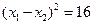
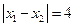
∴当
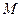 运动时,弦长
运动时,弦长 为定值4〕
为定值4〕
练习册系列答案
相关题目
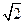 .记动点C的轨迹为曲线W.
.记动点C的轨迹为曲线W. 与
与 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.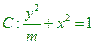 ;(1)由曲线C上任一点E向X轴作垂线,垂足为F,
;(1)由曲线C上任一点E向X轴作垂线,垂足为F,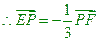 。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为
。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为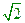 ,且过点
,且过点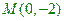 ,直线L交曲线C于A,B两点,又
,直线L交曲线C于A,B两点,又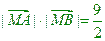 ,求曲线C的方程。
,求曲线C的方程。 
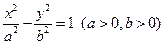 的一个焦点是
的一个焦点是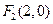 ,且
,且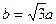 。
。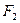 的直线
的直线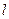 的一个法向量为
的一个法向量为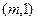 ,当直线
,当直线
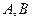 不同的两点时,求实数
不同的两点时,求实数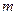 的取值范围;并证明
的取值范围;并证明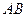 中点
中点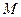 在曲线
在曲线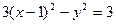 上。
上。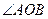 为锐角?若存在,请求出
为锐角?若存在,请求出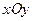 中的抛物线
中的抛物线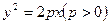 的焦点
的焦点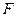 作一条倾斜角为
作一条倾斜角为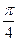 的直线与抛物线相交于A,B两点。
的直线与抛物线相交于A,B两点。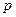 表示A,B之间的距离;
表示A,B之间的距离;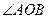 的大小是与
的大小是与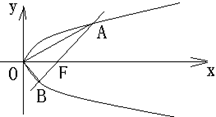
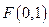 ,直线
,直线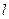 :
: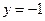 ,
,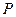 为平面上的动点,过点
为平面上的动点,过点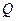 ,且
,且 .
.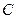 的方程;
的方程;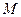 过定点
过定点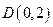 ,圆心
,圆心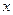 轴交于
轴交于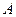 、
、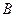 两点,设
两点,设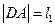 ,
, ,求
,求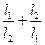 的最大值.
的最大值.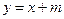 与双曲线
与双曲线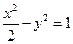 没有公共点,则实数
没有公共点,则实数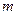 的取值范围是( )
的取值范围是( )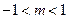
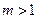 或
或