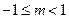题目内容
设椭圆C: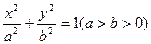 的左焦点为F,上顶点为A,过点A作垂直于AF的直线交椭圆C于另外一点P,交x轴正半轴于点Q,且
的左焦点为F,上顶点为A,过点A作垂直于AF的直线交椭圆C于另外一点P,交x轴正半轴于点Q,且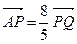
(1)求椭圆C的离心率;
(2)若过A、Q、F三点的圆恰好与直线l: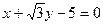 相切,求椭圆C的方程.
相切,求椭圆C的方程. 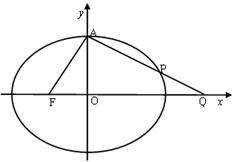
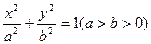 的左焦点为F,上顶点为A,过点A作垂直于AF的直线交椭圆C于另外一点P,交x轴正半轴于点Q,且
的左焦点为F,上顶点为A,过点A作垂直于AF的直线交椭圆C于另外一点P,交x轴正半轴于点Q,且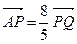
(1)求椭圆C的离心率;
(2)若过A、Q、F三点的圆恰好与直线l:
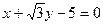 相切,求椭圆C的方程.
相切,求椭圆C的方程. 
(1)
(2)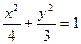
(2)
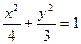
⑴设Q(x0,0),由F(-c,0)

A(0,b)知
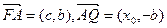
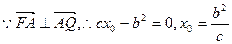 …2分
…2分设
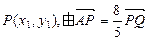 ,得
,得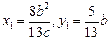 ………4分
………4分因为点P在椭圆上,所以
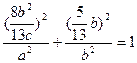 ………6分
………6分整理得2b2=3ac,即2(a2-c2)=3ac,
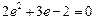 ,故椭圆的离心率e=………8分
,故椭圆的离心率e=………8分⑵由⑴知
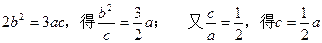 ,
,于是F(-a,0), Q
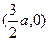
△AQF的外接圆圆心为(
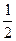 a,0),半径r=|FQ|=a…………10分
a,0),半径r=|FQ|=a…………10分所以
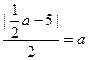 ,解得a=2,∴c=1,b=
,解得a=2,∴c=1,b=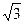 ,
,所求椭圆方程为

练习册系列答案
相关题目
 (
( 且
且 为常数),
为常数), 为其焦点.
为其焦点. 两点,且
两点,且 ,求直线
,求直线 的斜率;
的斜率; 是过抛物线焦点
是过抛物线焦点 ,如图所示.求四边形
,如图所示.求四边形 面积的最小值
面积的最小值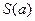 .
.
 图象上任意两个次整点作直线,则倾斜角大于45°的直线条数为.
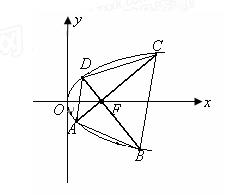
图象上任意两个次整点作直线,则倾斜角大于45°的直线条数为.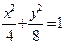 ,过原点且倾斜角为
,过原点且倾斜角为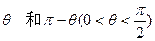 的两条直线分别交椭圆于A、C和B、D两点.(1)用
的两条直线分别交椭圆于A、C和B、D两点.(1)用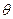 表示四边形ABCD的面积S;(2)当
表示四边形ABCD的面积S;(2)当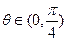 时,求S的最大值.
时,求S的最大值.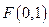 ,直线
,直线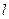 :
: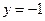 ,
,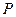 为平面上的动点,过点
为平面上的动点,过点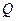 ,且
,且 .
.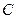 的方程;
的方程;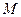 过定点
过定点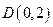 ,圆心
,圆心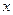 轴交于
轴交于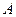 、
、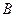 两点,设
两点,设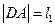 ,
, ,求
,求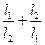 的最大值.
的最大值.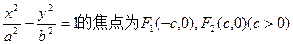 ,焦点F2到渐近线的距离为
,焦点F2到渐近线的距离为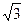 ,两条准线之间的距离为1。 (I)求此双曲线的方程; (II)过双曲线焦点F1的直线与双曲线的两支分别相交于A、B两点,过焦点F2且与AB平行的直线与双曲线分别相交于C、D两点,若A、B、C、D这四点依次构成平行四边形ABCD,且
,两条准线之间的距离为1。 (I)求此双曲线的方程; (II)过双曲线焦点F1的直线与双曲线的两支分别相交于A、B两点,过焦点F2且与AB平行的直线与双曲线分别相交于C、D两点,若A、B、C、D这四点依次构成平行四边形ABCD,且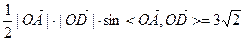 ,求直线AB的方程。
,求直线AB的方程。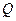 过点P(0,2), 且在
过点P(0,2), 且在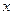 轴上截得的弦RG的长为4.
轴上截得的弦RG的长为4.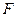 (0,1),作轨迹
(0,1),作轨迹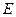 的两条互相垂直的弦
的两条互相垂直的弦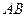 、
、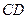 ,设
,设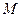 、
、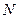 ,试判断直线
,试判断直线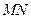 是否过定点?并说明理由.
是否过定点?并说明理由.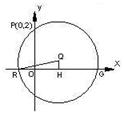
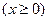 上
上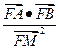 的值
的值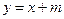 与双曲线
与双曲线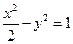 没有公共点,则实数
没有公共点,则实数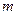 的取值范围是( )
的取值范围是( )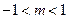
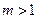 或
或