题目内容
(本小题满分13分)
已知抛物线 ,过点
,过点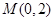 的直线
的直线 与抛物线交于
与抛物线交于 、
、 两点,且直线
两点,且直线 与
与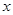 轴交于点
轴交于点 .(1)求证:
.(1)求证: ,
, ,
, 成等比数列;
成等比数列;
(2)设 ,
,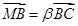 ,试问
,试问 是否为定值,若是,求出此定值;若不是,请说明理由.
是否为定值,若是,求出此定值;若不是,请说明理由.
已知抛物线
 ,过点
,过点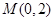 的直线
的直线 与抛物线交于
与抛物线交于 、
、 两点,且直线
两点,且直线 与
与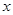 轴交于点
轴交于点 .(1)求证:
.(1)求证: ,
, ,
, 成等比数列;
成等比数列;(2)设
 ,
,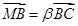 ,试问
,试问 是否为定值,若是,求出此定值;若不是,请说明理由.
是否为定值,若是,求出此定值;若不是,请说明理由.(1)见解析;
(2) 为定值且定值为
为定值且定值为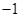
(2)
 为定值且定值为
为定值且定值为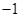
本试题主要是考查了解析几何与数列、不等式的综合运用。
(1)先设直线方程,然后利用题目中等比数列的关系得到各自的长度,进而证明。
(2)假设为定值,利用已知中向量的关系式,得到坐标关系,然后利用参数与坐标的关系表示得到证明。
解:(1)设直线 的方程为:
的方程为: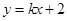
 ,
,
联立方程可得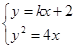 得:
得: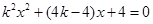 ① ………………………………2分
① ………………………………2分
设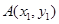 ,
,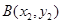 ,
,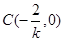 ,则
,则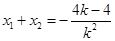 ,
,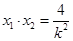 ②
②
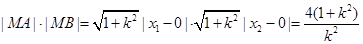 , …………………………4分
, …………………………4分
而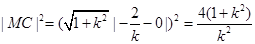 ,∴
,∴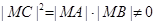 ,
,
即 ,
, 、
、 成等比数列…………………………………………………………6分
成等比数列…………………………………………………………6分
(2)法1:由 ,
,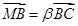 得,
得,
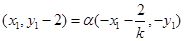 ,
,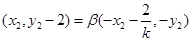
即得: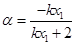 ,
,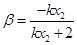 , ………………………………………………………8分
, ………………………………………………………8分
则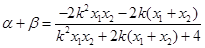 ………………………………………………………10分
………………………………………………………10分
由(1)中②代入得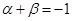 ,故
,故 为定值且定值为
为定值且定值为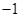 ………………………………13分
………………………………13分
法2:设直线 的方程为:
的方程为: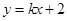
 ,
,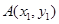 ,
,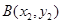 ,
,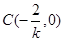 ,M(0,2)
,M(0,2)
联立方程可得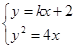 得:
得: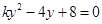 ………………………………………………8分由
………………………………………………8分由 ,
,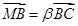 得,
得,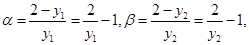 ………10分
………10分
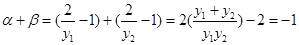 即证. ………………………………13分
即证. ………………………………13分
法3:设直线 的方程为:
的方程为: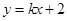
 ,
,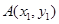 ,
,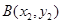 ,
,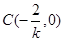 ,M(0,2)
,M(0,2)
由 得:
得: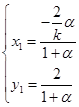 代入
代入 有:
有:
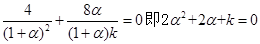 , 同理:
, 同理: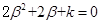 ,
,
所以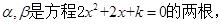 故
故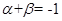 ………………………………13分(注:该法可以不联立直线与抛物线的方程.)
………………………………13分(注:该法可以不联立直线与抛物线的方程.)
(1)先设直线方程,然后利用题目中等比数列的关系得到各自的长度,进而证明。
(2)假设为定值,利用已知中向量的关系式,得到坐标关系,然后利用参数与坐标的关系表示得到证明。
解:(1)设直线
 的方程为:
的方程为: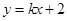
 ,
,联立方程可得
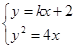 得:
得: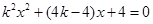 ① ………………………………2分
① ………………………………2分设
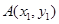 ,
,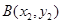 ,
,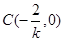 ,则
,则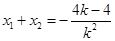 ,
,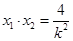 ②
②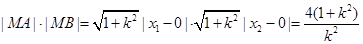 , …………………………4分
, …………………………4分而
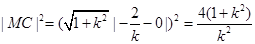 ,∴
,∴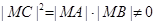 ,
,即
 ,
, 、
、 成等比数列…………………………………………………………6分
成等比数列…………………………………………………………6分(2)法1:由
 ,
,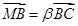 得,
得,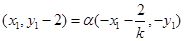 ,
,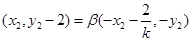
即得:
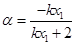 ,
,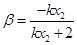 , ………………………………………………………8分
, ………………………………………………………8分则
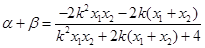 ………………………………………………………10分
………………………………………………………10分由(1)中②代入得
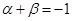 ,故
,故 为定值且定值为
为定值且定值为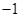 ………………………………13分
………………………………13分法2:设直线
 的方程为:
的方程为: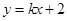
 ,
,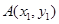 ,
,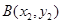 ,
,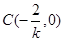 ,M(0,2)
,M(0,2)联立方程可得
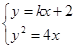 得:
得: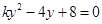 ………………………………………………8分由
………………………………………………8分由 ,
,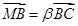 得,
得,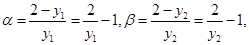 ………10分
………10分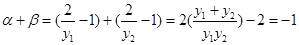 即证. ………………………………13分
即证. ………………………………13分法3:设直线
 的方程为:
的方程为: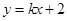
 ,
,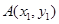 ,
,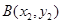 ,
,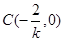 ,M(0,2)
,M(0,2)由
 得:
得: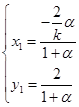 代入
代入 有:
有: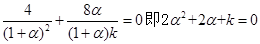 , 同理:
, 同理: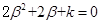 ,
,所以
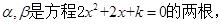 故
故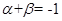 ………………………………13分(注:该法可以不联立直线与抛物线的方程.)
………………………………13分(注:该法可以不联立直线与抛物线的方程.)
练习册系列答案
相关题目

 ,过点
,过点 作抛物线
作抛物线 的切线,其切点分别为
的切线,其切点分别为 (其中
(其中 )。
)。 的值;
的值; 相切,求圆的面积。
相切,求圆的面积。 是曲线
是曲线 上的一个动点,曲线
上的一个动点,曲线 在点
在点 处的切线与
处的切线与 轴、
轴、 轴分别交于
轴分别交于 两点,点
两点,点 是坐标原点. 给出三个命题:①
是坐标原点. 给出三个命题:① ;②
;② 的周长有最小值
的周长有最小值 ;③曲线
;③曲线 ,使得
,使得 为等腰直角三角形.其中真命题的个数是
为等腰直角三角形.其中真命题的个数是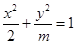 的离心率为
的离心率为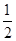 ,则m= ( )
,则m= ( ) 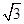
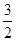
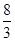
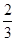
 >b>
>b> 的离心率为
的离心率为 且椭圆的一个焦点与抛物线
且椭圆的一个焦点与抛物线 的焦点重合,斜率为
的焦点重合,斜率为 的直线
的直线 过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴相交于点M(0,m).
过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴相交于点M(0,m).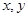 的方程
的方程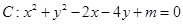 .
.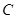 表示圆,求实数
表示圆,求实数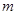 的取值范围 ;
的取值范围 ;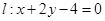 相交于
相交于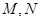 两点,且
两点,且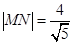 ,求
,求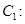
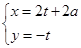 (
(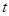 为参数),曲线
为参数),曲线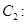
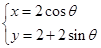 (
(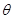 为参数).若曲线
为参数).若曲线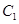 、
、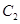 有公共点,则实数
有公共点,则实数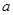 的取值范围_____.
的取值范围_____.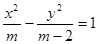 的左焦点与抛物线
的左焦点与抛物线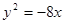 的焦点重合,则
的焦点重合,则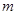 的值为
的值为