题目内容
若焦点在x轴上的椭圆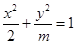 的离心率为
的离心率为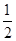 ,则m= ( )
,则m= ( )
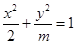 的离心率为
的离心率为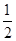 ,则m= ( )
,则m= ( ) A.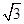 | B.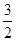 | C.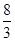 | D.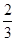 |
B
解:因为焦点在x轴上的椭圆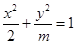 的离心率为
的离心率为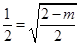 ,解得m=
,解得m=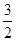 ,选B
,选B
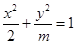 的离心率为
的离心率为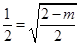 ,解得m=
,解得m=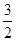 ,选B
,选B
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
题目内容
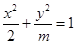 的离心率为
的离心率为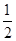 ,则m= ( )
,则m= ( ) A.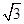 | B.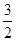 | C.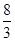 | D.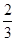 |
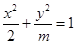 的离心率为
的离心率为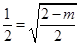 ,解得m=
,解得m=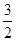 ,选B
,选B
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案