题目内容
13.下列四个结论:①设$\overrightarrow{a},\overrightarrow{b}$为向量,若$|\overrightarrow{a}•\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}|$,则$\overrightarrow{a}∥\overrightarrow{b}$恒成立;②命题“若x-sinx=0,则x=0”的逆命题为“若x≠0,则x-sinx≠0”;
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件;
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
分析 由向量的运算性质判断出夹角是90°即可判断①正确;由命题的逆否命题,先将条件、结论调换,再分别对它们否定,即可判断②;由命题p∨q为真,则p,q中至少有一个为真,不能推出p∧q为真,即可判断③.
解答 解:对于①设$\overrightarrow{a},\overrightarrow{b}$为向量,若$|\overrightarrow{a}•\overrightarrow{b}|=|\overrightarrow{a}||\overrightarrow{b}|$cos<$\overrightarrow{a}$,$\overrightarrow{b}$>,
从而cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=1,即$\overrightarrow{a}$和$\overrightarrow{b}$的夹角是90°,则$\overrightarrow{a}∥\overrightarrow{b}$恒成立,则①对;
对于②,命题“若x-sinx=0,则x=0”的逆否命题为“若x≠0,则x-sinx≠0”而不是逆命题,则②错;
对于③,命题p∨q为真,则p,q中至少有一个为真,不能推出p∧q为真,反之成立,
则应为必要不充分条件,则③错;
故选:A.
点评 本题考查了向量问题,考查复合命题的真假和真值表的运用,考查充分必要条件的判断和命题的否定,属于基础题和易错题.

练习册系列答案
相关题目
1.已知函数f(x+1)=3x+1,则f(x)的解析式为( )
| A. | f(x)=3-2x | B. | f(x)=2-3x | C. | f(x)=3x-2 | D. | f(x)=3x |
18.已知点A(1,2),B(4,3),向量$\overrightarrow{AC}=({-2,-2})$,则向量$\overrightarrow{BC}$=( )
| A. | (-5,-3) | B. | (5,3) | C. | (1,-1) | D. | (-1,-1) |
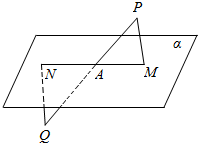 如图,已知直线PM∥QN,PM,QN分别与平面α交于M,N,直线PQ交平面α于A点.求证:M,N,A三点在同一条直线上.
如图,已知直线PM∥QN,PM,QN分别与平面α交于M,N,直线PQ交平面α于A点.求证:M,N,A三点在同一条直线上.