题目内容
3．
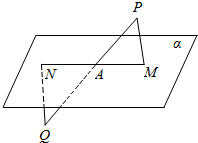如图，已知直线PM∥QN，PM，QN分别与平面α交于M，N，直线PQ交平面α于A点．求证：M，N，A三点在同一条直线上．
分析 由已知得平面PMNQ∩平面α=MN，A∈PQ，且A∈平面α，由此利用公理二能证明M，N，A三点在同一条直线上．
解答 证明：∵PM∥QN，∴PMNQ共面，
∵PM、QN分别与平面α交与M、N，
∴平面PMNQ∩平面α=MN，
∵直线PQ交平面α于A点，∴A∈PQ，且A∈平面α，
∴由公理二得A∈MN，
∴M，N，A三点在同一条直线上．
点评 本题考查三点共线的证明，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
8．若直线y=kx-1与双曲线x2-y2=1的左支有两个公共点，则k的取值范围是（ ）
| A． | （-$\sqrt{2}$，0） | B． | （-$\sqrt{2}$，$\sqrt{2}$） | C． | （-$\sqrt{2}$，-1） | D． | （-$\sqrt{2}$，-1] |
12．设函数f（x）=x3（x∈R），当0≤θ≤$\frac{π}{2}$时，f（cos2θ+2msinθ）+f（-2m-2）＜0恒成立，则实数m的取值范围是（ ）
| A． | （0，1） | B． | （-$\frac{1}{2}$，1） | C． | （-∞，1） | D． | （-$\frac{1}{2}$，+∞） |