题目内容
【题目】在如图所示的几何体中,D是AC的中点,EF∥DB. 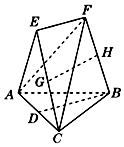
(1)已知AB=BC,AF=CF,求证:AC⊥平面BEF;
(2)已知G、H分别是EC和FB的中点,求证:GH∥平面ABC.
【答案】
(1)证明:∵EF∥DB,∴EF与DB确定平面BDEF.
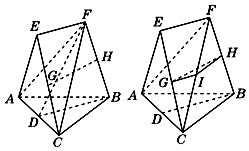
如图①,连结DF.∵AF=CF,D是AC的中点,∴DF⊥AC.同理可得BD⊥AC.
又BD∩DF=D,BD、DF平面BDEF,∴AC⊥平面BDEF,即AC⊥平面BEF.
(2)证明:如图②,设FC的中点为I,连接GI,HI.
在△CEF中,∵G分别是EC的中点,∴GI∥EF.
又EF∥DB,∴GI∥DB.
在△CFB中,∵H分别是FB的中点,∴HI∥BC.
又HI∩GI=I,∴平面GHI∥平面ABC.
∵GH平面GHI,∴GH∥平面ABC.
【解析】(1)如图连结DF,证明DF⊥AC,BD⊥AC.推出AC⊥平面BDEF,即可证明AC⊥平面BEF.(2)设FC的中点为I,连接GI,HI.证明GI∥EF.GI∥DB.证明HI∥BC.即可证明GHI∥平面ABC.然后证明GH∥平面ABC.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目