题目内容
【题目】等比数列{an}的前n项和为Sn , 已知对任意的n∈N+ , 点(n,Sn)均在函数y=bx+r(b>0且b≠1,b,r均为常数的图象上.
(1)求r的值.
(2)当b=2时,记bn=2(log2an+1)(n∈N+),证明:对任意的n∈N+,不等式成立 ![]() .
.
【答案】
(1)解:(1)因为对任意的n∈N+,点(n,Sn),
均在函数y=bx+r(b>0且b≠1,b,r均为常数的图象上.
所以得Sn=bn+r,当n=1时,a1=S1=b+r,
当n≥2时,an=Sn﹣Sn﹣1=bn+r﹣(bn﹣1+r)=bn﹣bn﹣1=(b﹣1)bn﹣1,
又因为{an}为等比数列,所以r=﹣1,公比为b,an=(b﹣1)bn﹣1
(2)当b=2时,an=(b﹣1)bn﹣1=2n﹣1,bn=2(log2an+1)=2(log22n﹣1+1)=2n
则 ![]() ,
,
所以 ![]()
下面用数学归纳法证明不等式 ![]()
![]() 成立.
成立.
当n=1时,左边= ![]() ,右边=
,右边= ![]() ,
,
因为 ![]() ,所以不等式成立.
,所以不等式成立.
假设当n=k时不等式成立,
即 ![]()
![]() 成立
成立
则当n=k+1时,
左边= ![]()
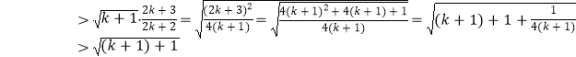
所以当n=k+1时,不等式也成立.
由①、②可得不等式恒成立
【解析】本题考查的数学归纳法及数列的性质.(1)由已知中因为对任意的n∈N+ , 点(n,Sn),均在函数y=bx+r(b>0且b≠1,b,r均为常数的图象上.根据数列中an与Sn的关系,我们易得到一个关于r的方程,再由数列{an}为等比数列,即可得到r的值.(2)将b=2代入,我们可以得到数列{an}的通项公式,再由bn=2(log2an+1)(n∈n),我们可给数列{bn}的通项公式,进而可将不等式 ![]() 进行简化,然后利用数学归纳法对其进行证明.
进行简化,然后利用数学归纳法对其进行证明.
【考点精析】根据题目的已知条件,利用数学归纳法的定义的相关知识可以得到问题的答案,需要掌握数学归纳法是证明关于正整数n的命题的一种方法.