题目内容
15.函数y=xcosx+sinx的图象大致为( )| A. |  | B. | 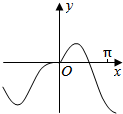 | C. |  | D. |  |
分析 给出的函数是奇函数,奇函数图象关于原点中心对称,由此排除B,然后利用区特值排除A和C,则答案可求.
解答 解:由于函数y=xcosx+sinx为奇函数,
故它的图象关于原点对称,所以排除选项B,
由当x=$\frac{π}{2}$时,y=1>0,
当x=π时,y=π×cosπ+sinπ=-π<0.
由此可排除选项A和选项C.
故正确的选项为D.
故选:D.
点评 本题主要考查了函数的图象,考查了函数的性质,考查了函数的值,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.设f′(x)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
| A. | 不存在 | B. | 与x轴平行或重合 | C. | 与x轴垂直 | D. | 与x轴相交不垂直 |
6.函数f(x)=$\frac{x-1}{{{x^2}+x+2}}$(2<x<4)的值域为( )
| A. | $(-∞,\frac{1}{7}]$ | B. | $[\frac{1}{8},\frac{1}{7}]$ | C. | $(\frac{1}{8},\frac{1}{7}]$ | D. | $(0,\frac{1}{7}]$ |
3.下面给出了关于复数的三种类比推理:
①复数的加减法运算法则可以类比多项式的加减法运算法则;
②由实数可以比较大小类比得到复数也可以比较大小;
③由向量加法的几何意义可以类比得到复数加法的几何意义;
其中正确的类比是( )
①复数的加减法运算法则可以类比多项式的加减法运算法则;
②由实数可以比较大小类比得到复数也可以比较大小;
③由向量加法的几何意义可以类比得到复数加法的几何意义;
其中正确的类比是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
20.设函数F(x)=$\frac{f(x)}{{e}^{x}}$是定义在R上的函数,其中f(x)的导函数为f′(x),满足f′(x)<f(x)对于x∈R恒成立,则( )
| A. | f(2)>e2f(0),f(2012)<e2012f(0) | B. | f(2)<e2f(0),f(2012)<e2012f(0) | ||
| C. | f(2)>e2f(0),f(2012)>e2012f(0) | D. | f(2)<e2f(0),f(2012)>e2012f(0) |