题目内容

5．设f′（x）=0，则曲线y=f（x）在点（x0，f（x0））处的切线（　　）
A．不存在B．与x轴平行或重合C．与x轴垂直D．与x轴相交不垂直

分析 根据题意和导数的几何意义求出在点（x0，f（x0））处的切线斜率，即可得到答案．

解答 解：由题意得，f′（x）=0，
∴在点（x0，f（x0））处的切线斜率是0，
∴在点（x0，f（x0））处的切线与x轴平行或重合，
故选：B．

点评 本题考查了导数的几何意义，即点P处的切线的斜率是该点出的导数值，属于基础题．

练习册系列答案
相关题目
14．在平面直角坐标系xoy中，已知经过原点O的直线l与圆C：x2+y2-4x-1=0交于A，B两点．
（1）若直线m：ax-2y+a+2=0（a＞0）与圆C相切，切点为B，求直线l的方程；
（2）若OB=2OA，求直线l的方程；
（3）若圆C与x轴的正半轴的交点为D，求△ABD面积的最大值．
16．圆x2+y2-4x+6y=0的半径r=$\sqrt{13}$．
13．sin（-120°）的值为（　　）
A．$\frac{1}{2}$B．$\frac{{\sqrt{3}}}{2}$C．$-\frac{1}{2}$D．$-\frac{{\sqrt{3}}}{2}$
20．已知抛物线y=-x2+4x-3及其上两点A（0，-3），B（3，0），
（1）分别求抛物线在A，B两点处的切线方程；
（2）求由抛物线及其在A，B两点处的切线共同围成的图形的面积．
10．已知双曲线与椭圆$\frac{x^2}{64}+\frac{y^2}{16}=1$有相同的焦点，若双曲线的一条渐近线方程是$x+\sqrt{3}y=0$，则双曲线的方程为$\frac{{x}^{2}}{36}-\frac{{y}^{2}}{12}=1$．
17．在三角形△ABC中，内角A，B，C所对的边分别为a，b，c，且2c2=2a2+2b2+ab，则△ABC的形状是（　　）
A．锐角三角形B．钝角三角形C．等腰三角形D．等边三角形
14．已知tanα=3，求$\frac{4sinα-cosα}{3sinα+5cosα}$的值．
15．函数y=xcosx+sinx的图象大致为（　　）
A．B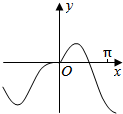．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网