题目内容

5．已知等比数列{an}的各项均为正数，且a1=1，a2+a3=6，求该数列的前n项和为Sn．

分析 根据所给的数列首项和a2+a3=6，整理出关于公比q的一元二次方程，解方程得到两个解，舍去负解，即可求出数列的前n项和．

解答 解：设等比数列{an}的公比为q，
则q＞0，
∵a1=1，a2+a3=6，
∴q+q2=6，
即，q2+q-6=0，
解得：q=2，q=-3（舍去），
∴Sn=$\frac{{a}_{1}（1-{q}^{n}）}{1-q}$=$\frac{1-{2}^{n}}{1-2}$=2n-1．

点评 本题考查等比数列的通项公式，解题的关键是数列中基本量的运算，求出数列的公比是解决本题的关键．

练习册系列答案
相关题目
15．函数y=xcosx+sinx的图象大致为（　　）
A．B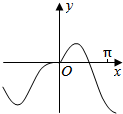．C．D．
16．在复平面内，复数1-$\frac{1}{i}$所对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
13．在极坐标系中，已知一个圆的方程为ρ=12sin（θ-$\frac{π}{6}$），则经过圆心且和极轴垂直的直线的极坐标方程是（　　）
A．ρsinθ=3$\sqrt{3}$B．ρsinθ=-3$\sqrt{3}$C．ρcosθ=-3D．ρsinθ=3
20．已知函数f（x）=2sin（2x+$\frac{π}{6}$）（x∈R）
（1）求f（$\frac{π}{4}$）的值；
（2）若△ABC中，A=$\frac{π}{4}$，f（$\frac{B}{2}$+$\frac{π}{6}$）=$\frac{8}{5}$，求f（$\frac{C}{2}$-$\frac{π}{12}$）
10．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知csinA=$\sqrt{3}$acosC．
（1）求角C的大小；
（2）c=$\sqrt{7}$，A≠$\frac{π}{2}$，sinC+sin（B-A）=3sin2A，求△ABC的面积．
17．已知数列{an}的首项a1=$\frac{1}{4}$的等比数列，其前n项和Sn中，S3，S4，S2成等差数列，
（1）求数列{an}的通项公式；
（2）设bn=log${\;}_{\frac{1}{2}}$|an|，记数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和为Tn，若Tn≤λbn+1对一切n∈N*恒成立，求实数λ的最小值．
14．已知常数λ∈R，且λ≠0，数列{an}满足a1=$\frac{1}{3}$，an+1=$\frac{λ{a}_{n}}{2{a}_{n}+1}$，n∈N*．
（1）若λ=1，求证：数列{$\frac{1}{{a}_{n}}$}为等差数列；
（2）若λ=2，求证：数列{$\frac{1}{{a}_{n}}$-2}为等比数列；
（3）是否存在实数λ与前n项和为Sn的等比数列{bn}，使得对任意n∈N*，an=$\frac{{b}_{n}}{{S}_{n}+2}$恒成立？如果存在，求出λ与数列{bn}的通项公式；如果不存在，请说明理由．
15．圆C1：（x-3）2+y2=1，圆C2：（x+3）2+y2=4，若圆M与两圆都相切，则圆心M的轨迹是（　　）
A．两个椭圆B．两条双曲线
C．两条双曲线的左支D．两条双曲线的右支

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网