题目内容
20.设函数F(x)=$\frac{f(x)}{{e}^{x}}$是定义在R上的函数,其中f(x)的导函数为f′(x),满足f′(x)<f(x)对于x∈R恒成立,则( )| A. | f(2)>e2f(0),f(2012)<e2012f(0) | B. | f(2)<e2f(0),f(2012)<e2012f(0) | ||
| C. | f(2)>e2f(0),f(2012)>e2012f(0) | D. | f(2)<e2f(0),f(2012)>e2012f(0) |
分析 求函数F(x)=$\frac{f(x)}{{e}^{x}}$的导数,判断函数的单调性,利用单调性进行判断即可.
解答 解:∵F(x)=$\frac{f(x)}{{e}^{x}}$,
∴函数的导数F′(x)=$\frac{f′(x){e}^{x}-f(x){e}^{x}}{({e}^{x})^{2}}$=$\frac{f′(x)-f(x)}{{e}^{x}}$,
∵f′(x)<f(x),
∴F′(x)<0,
即函数F(x)是减函数,
则F(0)>F(2),F(0)>F(2012),
即$\frac{f(0)}{{e}^{0}}>\frac{f(2)}{{e}^{2}}$,$\frac{f(0)}{{e}^{0}}$>$\frac{f(2012)}{{e}^{2012}}$
即f(2)<e2f(0),f(2012)<e2012f(0),
故选:B
点评 本题主要考查函数值的大小比较,根据条件求函数的导数,判断函数的单调性是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下列求导数运算错误的是( )
| A. | (3x)′=3xln3 | |
| B. | (x2lnx)′=2xlnx+x | |
| C. | $(\frac{cosx}{x})'=\frac{xsinx-cosx}{x^2}$ | |
| D. | $({2^{ln({x^2}+1)}})'=\frac{2xln2}{{{x^2}+1}}•{2^{ln({x^2}+1)}}$ |
8.如果复数z满足|z+3i|+|z-3i|=6,那么|z+1+i|的最小值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
15.函数y=xcosx+sinx的图象大致为( )
| A. | 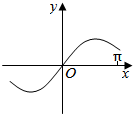 | B. | 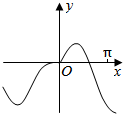 | C. | 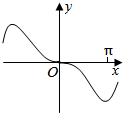 | D. | 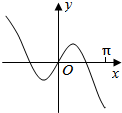 |