题目内容
10.用反证法证明:若三个互不相等的正数,a,b,c成等差数列,求证:a,b,c不可能成等比数列.分析 假设a,b,c成等比数列,则b2=ac,由等差数列的性质可得b=$\frac{a+c}{2}$,能推出a=c与三个互不相等的正数矛盾,即可得出结论.
解答 证明:假设a,b,c成等比数列,则b2=ac,
∵a,b,c成等差数列,
∴b=$\frac{a+c}{2}$,
∴($\frac{a+c}{2}$)2=ac,
∴(a-c)2=0,
∴a=c,
与三个互不相等的正数矛盾,
∴假设不成立,
∴a,b,c不可能成等比数列.
点评 本题考查用反证法证明不等式,用反证法证明不等式的关键是推出矛盾.

练习册系列答案
相关题目
18.设x、y满足约束条件$\left\{\begin{array}{l}{x+y≤1}\\{y≥x}\\{x≥0}\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
5.已知函数y=logax(a>0,a≠1)的图象经过点(4,$\frac{1}{2}$),则a的值为( )
| A. | 16 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
15.函数y=xcosx+sinx的图象大致为( )
| A. |  | B. | 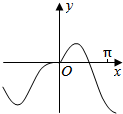 | C. |  | D. |  |