题目内容
6.函数f(x)=$\frac{x-1}{{{x^2}+x+2}}$(2<x<4)的值域为( )| A. | $(-∞,\frac{1}{7}]$ | B. | $[\frac{1}{8},\frac{1}{7}]$ | C. | $(\frac{1}{8},\frac{1}{7}]$ | D. | $(0,\frac{1}{7}]$ |
分析 求f′(x)=$\frac{-{x}^{2}+2x+3}{({x}^{2}+x+2)^{2}}$,而f′(x)=0的解为x=-1,或3,从而可判断f′(x)在区间(2,4]上的符号,从而可得出f(x)的最大值为f(3),再比较f(2)和f(4)的大小,这样便可得出函数f(x)的值域.
解答 解:f′(x)=$\frac{-{x}^{2}+2x+3}{({x}^{2}+x+2)^{2}}$;
∴2<x<3时,f′(x)>0,3<x<4时,f′(x)<0;
∴x=3时f(x)取最大值f(3)=$\frac{1}{7}$;
又f(2)=$\frac{1}{8}$,f(4)=$\frac{3}{22}$$>\frac{1}{8}$;
∴$\frac{1}{8}<f(x)≤\frac{1}{7}$;
∴f(x)的值域为$(\frac{1}{8},\frac{1}{7}]$.
故选C.
点评 考查商的求导公式,根据导数求函数最大值的方法,以及根据导数求函数值域的方法与过程,熟练一元二次不等式的解法.

练习册系列答案
相关题目
17.在三角形△ABC中,内角A,B,C所对的边分别为a,b,c,且2c2=2a2+2b2+ab,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
11.下列求导数运算错误的是( )
| A. | (3x)′=3xln3 | |
| B. | (x2lnx)′=2xlnx+x | |
| C. | $(\frac{cosx}{x})'=\frac{xsinx-cosx}{x^2}$ | |
| D. | $({2^{ln({x^2}+1)}})'=\frac{2xln2}{{{x^2}+1}}•{2^{ln({x^2}+1)}}$ |
18.设x、y满足约束条件$\left\{\begin{array}{l}{x+y≤1}\\{y≥x}\\{x≥0}\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
15.函数y=xcosx+sinx的图象大致为( )
| A. |  | B. | 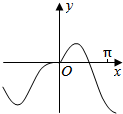 | C. |  | D. |  |
16.在复平面内,复数1-$\frac{1}{i}$所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |