题目内容
【题目】已知a,b为正实数,函数f(x)=ax3+bx+2x在[0,1]上的最大值为4,则f(x)在[﹣1,0]上的最小值为
【答案】![]()
【解析】∵a,b为正实数,函数f(x)=ax3+bx+2x ,
∴f(x)在R上是增函数,
∴f(x)在[0,1]上的最大值f(1)=a+b+2=4,
∴a+b=2.
∴f(x)在[﹣1,0]上的最小值f(﹣1)=﹣(a+b)+2﹣1=﹣2+![]() =
=![]() .
.
∴f(x)在[﹣1,0]上的最小值是![]()
所以答案是:![]()
【考点精析】根据题目的已知条件,利用函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
(Ⅰ)在给定的坐标系中画出表中数据的散点图;

(Ⅱ)试对![]() 与
与![]() 的关系进行相关性检验,如
的关系进行相关性检验,如![]() 与
与![]() 具有线性相关关系,求出
具有线性相关关系,求出![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(Ⅲ)试预测加工![]() 个零件需要多少时间?
个零件需要多少时间?
参考数据:![]() ,
,![]() .
.
附: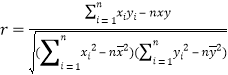 );
); ,
, ![]() ;
;
相关性检验的临界值表
n-2 | 小概率 | n-2 | 小概率 | n-2 | 小概率 | |||
0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | |||
1 | 0.997 | 1 | 4 | 0.811 | 0.917 | 7 | 0.666 | 0.798 |
2 | 0.950 | 0.990 | 5 | 0.754 | 0.874 | 8 | 0.632 | 0.765 |
3 | 0.878 | 0.959 | 6 | 0.707 | 0.834 | 9 | 0.602 | 0.735 |
注:表中的n为数据的组数
