题目内容
【题目】已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x﹣1.
(1)求f(x)的函数解析式,并用分段函数的形式给出;
(2)作出函数f(x)的简图;
(3)写出函数f(x)的单调区间及最值.
【答案】
(1)解:当x<0时,﹣x>0,
则f(﹣x)=(﹣x)2﹣2(﹣x)﹣1=x2+2x﹣1,
∵f(x)是偶函数,
∴f(x)=f(﹣x)=x2+2x﹣1,
∴f(x)= ![]()
(2)解:函数f(x)的简图:
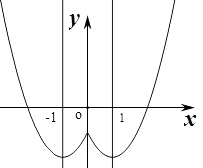
(3)解:单调增区间为[﹣1,0]和[1,+∞),
单调减区间为(﹣∞,﹣1]和[0,1],
当x=1或﹣1时,f(x)有最小值﹣2.
【解析】(1)利用函数的奇偶性求f(x)的函数解析式,并用分段函数的形式给出;(2)结合函数的表达式进行作图;(3)根据函数的表达式写出函数f(x)的单调区间及最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目