题目内容
【题目】选修4-4：坐标系与参数方程
已知曲线
的极坐标方程为
，直线
，直线
.以极点
为原点，极轴为
轴正半轴建立平面直角坐标系.
(1)求直线
的直角坐标方程以及曲线的参数方程；
(2)已知直线
与曲线交于
两点，直线
与曲线交于
两点，求
的周长.
【答案】（1）见解析（2）
【解析】试题分析 ：(1)直线
，所以斜率
，过（0，0），直角坐标方程为
，同理可求的
的直角坐标方程为
.
两边同时乘以
，得
，再由
，代入可得故
，所以圆过（2，1），r=
,曲线
的参数方程为
（
为参数）.
(2) 直接利用极坐标方程联立求解，先联立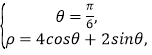
得到
，同理
.又
，所以
,可解。
试题解析：（1）依题意，直线
的直角坐标方程为，直线的直角坐标方程为.
因为，故，故
，故，
故曲线的参数方程为（为参数）
（2）联立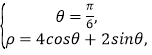得到，同理.
又，所以
，
即
的面积为
.
练习册系列答案
口算能手系列答案
相关题目
【题目】某校有150名学生参加了中学生环保知识竞赛，为了解成绩情况，现从中随机抽取50名学生的成绩进行统计（所有学生成绩均不低于60分）.请你根据尚未完成的频率分布表，解答下列问题：
（1）写出M 、N 、p、q（直接写出结果即可），并作出频率分布直方图；
（2）若成绩在90分以上学生获得一等奖，试估计全校所有参赛学生获一等奖的人数；
（3）现从所有一等奖的学生中随机选择2名学生接受采访，已知一等奖获得者中只有2名女生，求恰有1名女生接受采访的概率.
分组 | 频数 | 频率 | |
第1组 | [60,70) | M | 0.26 |
第2组 | [70,80) | 15 | p |
第3组 | [80,90) | 20 | 0.40 |
第4组 | [90,100] | N | q |
合计 | 50 | 1 | |
【题目】 由经验得知，在某商场付款处排队等候付款的人数及概率如下表
排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
(1)至多有2人排队的概率是多少?
(2)至少有2人排队的概率是多少?
