题目内容
1.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左,右焦点分别为F1(-1,0),F2(1,0),椭圆C的上顶点与右顶点的距离为$\sqrt{3}$,过F2的直线与椭圆C交于A,B两点.(Ⅰ)求椭圆C的方程
(Ⅱ)点M在直线x=2上,直线MA,MB的斜率分别为k1,k2,若k1+k2=2,求证:点M为定点.
分析 (Ⅰ)由椭圆的焦点坐标和a,b,c的关系,可得a,b,进而得到椭圆方程;
(Ⅱ)若直线AB斜率不存在,AB:x=1.求得A,B,M的坐标,求得MA.MB的斜率,解方程可得m=1;若直线AB斜率存在,设为k,设直线AB方程为:y=k(x-1),A(x1,y1),B(x2,y2),M(2,m),联立椭圆方程,运用韦达定理和直线的斜率公式,化简整理,解方程即可得到m=1,进而得到定点M.
解答 解:(Ⅰ)由题意知:$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=3}\\{{a}^{2}-{b}^{2}=1}\end{array}\right.$,可得a2=2,b2=1,
则椭圆方程为$\frac{{x}^{2}}{2}$+y2=1;
(Ⅱ)证明:若直线AB斜率不存在,AB:x=1.
不妨设A(1,$\frac{\sqrt{2}}{2}$),B(1,-$\frac{\sqrt{2}}{2}$),M(2,m),
则k1=$\frac{m-\frac{\sqrt{2}}{2}}{2-1}$=m-$\frac{\sqrt{2}}{2}$,k2=$\frac{m+\frac{\sqrt{2}}{2}}{2-1}$=m+$\frac{\sqrt{2}}{2}$,
由k1+k2=2,可得2m=2,即m=1,
若直线AB斜率存在,设为k,
设直线AB方程为:y=k(x-1),A(x1,y1),B(x2,y2),M(2,m),
$\left\{\begin{array}{l}{y=k(x-1)}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$可得(1+2k2)x2-4k2x+2(k2-1)=0,
x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2({k}^{2}-1)}{1+2{k}^{2}}$,
k1=$\frac{k({x}_{1}-1)-m}{{x}_{1}-2}$,k2=$\frac{k({x}_{2}-1)-m}{{x}_{2}-2}$,
k1+k2=$\frac{2k{x}_{1}{x}_{2}-(3k+m)({x}_{1}+{x}_{2})+4(k+m)}{{x}_{1}{x}_{2}-2({x}_{1}+{x}_{2})+4}$
=$\frac{4{k}^{2}m+4m}{2({k}^{2}+1)}$=2,
所以m=1,
所以定点M(2,1).
点评 本题考查椭圆的方程和性质,主要考查椭圆方程的运用,联立直线方程,运用韦达定理,以及直线的斜率公式,化简整理,属于中档题.

| A. | $\frac{π}{6}≤θ≤\frac{π}{2}$ | B. | $\frac{π}{3}≤θ≤\frac{π}{2}$ | C. | $0≤θ≤\frac{π}{3}$ | D. | $0<θ<\frac{2π}{3}$ |
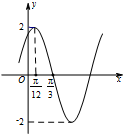 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.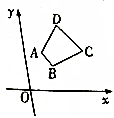 已知梯形ABCD,如图所示,其中AB∥CD,且DC=2AB,三个顶点的坐标分别为A(1,2)、B(2,1)、C(4,2),求点D的坐标.
已知梯形ABCD,如图所示,其中AB∥CD,且DC=2AB,三个顶点的坐标分别为A(1,2)、B(2,1)、C(4,2),求点D的坐标.