题目内容
8.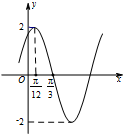 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.(1)求函数f(x)的解析式;
(2)在△ABC中,角A,B,C的对边分别为a,b,c,f(A-$\frac{π}{3}$)=$\sqrt{3}$,且角A为锐角,b+c=2a=2$\sqrt{3}$,求△ABC的面积并判断△ABC的形状.
分析 (1)首先,根据图象得到振幅和A=2,ω=2,从而得到f(x)=2sin(2x+φ),然后,将点($\frac{π}{12}$,2)代入得到φ=$\frac{π}{3}$,从而可求解析式;
(2)由f(A-$\frac{π}{3}$)=$\sqrt{3}$,结合0$<A<\frac{π}{2}$,可解得A=$\frac{π}{3}$,由b+c=2a=2$\sqrt{3}$,两边平方可得:b2+c2=12-2bc①,由余弦定理cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$可得:b2+c2=a2+bc=3+bc②,由①②可得:bc=3,结合已知b+c=2$\sqrt{3}$,可解得b=c=a=$\sqrt{3}$,从而可求△ABC为等边三角形,即可求得面积.
解答 解:(1)根据图象得到:A=2,$\frac{T}{4}$=$\frac{π}{3}-\frac{π}{12}=\frac{π}{4}$,
∴T=π,
∴$\frac{2π}{ω}=π$,
∴ω=2,
∴f(x)=2sin(2x+φ),
将点($\frac{π}{12}$,2)代入得到2sin($\frac{π}{6}$+φ)=2,|φ|<$\frac{π}{2}$
∴φ=$\frac{π}{3}$,
∴f(x)=2sin(2x+$\frac{π}{3}$).
(2)∵f(A-$\frac{π}{3}$)=2sin(2A-$\frac{2π}{3}$+$\frac{π}{3}$)=2sin(2A-$\frac{π}{3}$)=$\sqrt{3}$,
∴sin(2A-$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$,
∵0$<A<\frac{π}{2}$,∴-$\frac{π}{3}$<2A-$\frac{π}{3}$<$\frac{2π}{3}$,故解得:2A-$\frac{π}{3}$=$\frac{π}{3}$,既有:A=$\frac{π}{3}$,
∵b+c=2a=2$\sqrt{3}$,∴两边平方可得:b2+c2=12-2bc①,
∵由余弦定理cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$可得:b2+c2=a2+bc=3+bc②
∴由①②可得:bc=3,结合已知,b+c=2$\sqrt{3}$可得:(2$\sqrt{3}-b$)b=3,解得:b=c=a=$\sqrt{3}$,
∴△ABC为等边三角形.
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×3×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$.
点评 本题重点考查了三角函数的图象与性质及其运用,考查了余弦定理的综合应用,属于基本知识的考查.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 如图,在△ABC中,已知点D在BC边上,cos∠ADC=$\frac{\sqrt{2}}{3}$,cos∠BAD=$\frac{\sqrt{3}}{3}$,AD=2,则BA的长为( )
如图,在△ABC中,已知点D在BC边上,cos∠ADC=$\frac{\sqrt{2}}{3}$,cos∠BAD=$\frac{\sqrt{3}}{3}$,AD=2,则BA的长为( )| A. | $\frac{14\sqrt{3}+4\sqrt{21}}{3}$ | B. | 7$\sqrt{3}$+4 | C. | $\sqrt{3}$+4$\sqrt{7}$ | D. | 7+4$\sqrt{7}$ |
 如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.
如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.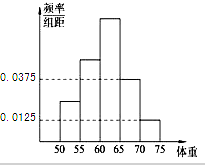 某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.