题目内容
16.已知向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为θ,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则θ的取值范围是( )| A. | $\frac{π}{6}≤θ≤\frac{π}{2}$ | B. | $\frac{π}{3}≤θ≤\frac{π}{2}$ | C. | $0≤θ≤\frac{π}{3}$ | D. | $0<θ<\frac{2π}{3}$ |
分析 根据|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,两边平方可求,${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}$,$\overrightarrow{a}•\overrightarrow{b}$,由夹角公式可得,cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{\frac{1}{2}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{1}{4}×\frac{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}}{|\overrightarrow{a}||\overrightarrow{b}|}$,利用基本不等式可求cosθ,从而得到θ的取值范围.
解答 解:∵|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=1,
∴${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}=3$,${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}-2\overrightarrow{a}•\overrightarrow{b}=1$,
解可得,${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}$=2,$\overrightarrow{a}•\overrightarrow{b}$=$\frac{1}{2}$,
∵cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{\frac{1}{2}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{1}{4}×\frac{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}}{|\overrightarrow{a}||\overrightarrow{b}|}$$≥\frac{1}{4}×\frac{2|\overrightarrow{a}||\overrightarrow{b}|}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{1}{2}$
又∵0≤θ≤π
∴0$≤θ≤\frac{1}{3}π$
故选C
点评 本题综合考查了平面向量的基本运算,基本不等式及其运用等知识,属于中档题

 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案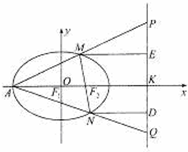 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.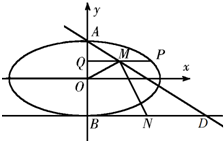 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.