题目内容
9.已知点列T:P1(x1,y1),P2(x2,y2),…Pk(xk,yk) (k∈N*,k≥2)满足P1(1,1),$\left\{\begin{array}{l}{{x}_{i}={x}_{i-1}+1}\\{{y}_{i}={y}_{i-1}}\end{array}\right.$与$\left\{\begin{array}{l}{{x}_{i}={x}_{i-1}}\\{{y}_{i}={y}_{i-1}+1}\end{array}\right.$(i=2,3,4…k)中有且只有一个成立.(1)写出满足k=4的所有点列;
(2)证明:对于任意给定的k(k∈N*,k≥2),不存在点列T,使得$\sum_{i=1}^{k}{x}_{i}$+$\sum_{i=1}^{k}{y}_{i}$=2k;
(3)当k=2n-1且P2n-1(n,n)(n∈N*,n≥2)时,求$\sum_{i=1}^{k}{x}_{i}×\sum_{i=1}^{k}{y}_{i}$ 的最大值.
分析 (1)由新数列的定义,列举即可得到;
(2)首先判断数列{xi+yi}是公差为1的等差数列,再假设存在点列T,使得$\sum_{i=1}^{k}{x}_{i}$+$\sum_{i=1}^{k}{y}_{i}$=2k,即$\frac{1}{2}$k(k+3)=2k,推出矛盾即可得证;
(3)化简整理,可令t=x1+x2+…+x2n-1,则$\sum_{i=1}^{k}{x}_{i}×\sum_{i=1}^{k}{y}_{i}$=t[(n+1)(2n-1)-t],考虑f(t)=t[(n+1)(2n-1)-t],①当n为奇数时,可得$\frac{1}{2}$(n+1)(2n-1)为正整数,②当n为偶数时,可得$\frac{1}{2}$(n+1)(2n-1)不为正整数,$\frac{1}{2}$(n+1)(2n-1)-$\frac{1}{2}$是离其最近的正整数,构造数列,即可得到结论.
解答 解:(1)符合条件的点列T为:P1(1,1),P2(1,2),P3(2,2),P4(3,2),
或P1(1,1),P2(2,1),P3(2,2),P4(3,2),
或P1(1,1),P2(2,1),P3(3,1),P4(3,2);
(2)证明:由已知xi+yi=xi-1+yi-1+1,则数列{xi+yi}是公差为1的等差数列,
由x1+y1=2,可得xi+yi=i+1(i=1,2,…,k),
$\sum_{i=1}^{k}{x}_{i}$+$\sum_{i=1}^{k}{y}_{i}$=$\sum_{i=1}^{k}$(xi+yi)=2+3+…+(k+1)=$\frac{1}{2}$k(k+3),
若存在点列T,使得$\sum_{i=1}^{k}{x}_{i}$+$\sum_{i=1}^{k}{y}_{i}$=2k,即$\frac{1}{2}$k(k+3)=2k,即k(k+3)=2k+1,
由k和k+3一个为奇数,一个为偶数,且k≥2,而整数2k+1不含大于1的奇因子,
故对于任意给定的k(k∈N*,k≥2),不存在点列T,使得$\sum_{i=1}^{k}{x}_{i}$+$\sum_{i=1}^{k}{y}_{i}$=2k;
(3)由已知yi=i+1-xi(i=1,2,…,2n-1),
$\sum_{i=1}^{k}{x}_{i}×\sum_{i=1}^{k}{y}_{i}$=(x1+x2+…+x2n-1)(2-x1+3-x2+…+2n-x2n-1)
=(x1+x2+…+x2n-1)((2+3+…+2n)-(x1+x2+…+x2n-1)),
令t=x1+x2+…+x2n-1,则$\sum_{i=1}^{k}{x}_{i}×\sum_{i=1}^{k}{y}_{i}$=t[(n+1)(2n-1)-t],
考虑f(t)=t[(n+1)(2n-1)-t],
①当n为奇数时,可得$\frac{1}{2}$(n+1)(2n-1)为正整数,
构造数列{xi}:1,2,…,$\frac{1}{2}$(n+1),…,$\frac{1}{2}$(n+1),$\frac{1}{2}$(n+1)+1,…,n,
对应数列{yi}:1,1,…,1,2,…,n,…,n.
而此时x1+x2+…+x2n-1,=1+2+…+n+$\frac{1}{2}$(n+1)+$\frac{1}{2}$(n+1)+…+$\frac{1}{2}$(n+1)=1+2+…+n+$\frac{1}{2}$(n+1)(n-1)
=$\frac{1}{2}$(n+1)(2n-1),
所以t=$\frac{1}{2}$(n+1)(2n-1),$\sum_{i=1}^{k}{x}_{i}×\sum_{i=1}^{k}{y}_{i}$ 的最大值为$\frac{1}{4}$(n+1)2(2n-1)2;
②当n为偶数时,可得$\frac{1}{2}$(n+1)(2n-1)不为正整数,$\frac{1}{2}$(n+1)(2n-1)-$\frac{1}{2}$是离其最近的正整数,
构造数列{xi}:1,2,…,$\frac{1}{2}$n,…,$\frac{1}{2}$n,$\frac{1}{2}$n+1,$\frac{1}{2}$n+2,…,n,
对应数列{yi}:1,1,…,1,2,…,$\frac{1}{2}$n+1,$\frac{1}{2}$n+1,$\frac{1}{2}$n+2,…,$\frac{1}{2}$n+$\frac{1}{2}$n,…,n.
而此时x1+x2+…+x2n-1,=1+2+…+n+$\frac{1}{2}$n+…+$\frac{1}{2}$n+$\frac{1}{2}$n+1…+$\frac{1}{2}$n+1=
$\frac{1}{2}$(n+1)(2n-1)-$\frac{1}{2}$,
所以t=$\frac{1}{2}$(n+1)(2n-1)-$\frac{1}{2}$,$\sum_{i=1}^{k}{x}_{i}×\sum_{i=1}^{k}{y}_{i}$ 的最大值为$\frac{1}{4}$(n+1)2(2n-1)2-$\frac{1}{4}$.
点评 本题考查递推数列的求和,同时考查考查等差数列的求和公式,理解新数列和分类讨论的思想方法是解题的关键,属于难题.

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案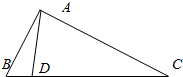 如图,在△ABC中,已知点D在BC边上,cos∠ADC=$\frac{\sqrt{2}}{3}$,cos∠BAD=$\frac{\sqrt{3}}{3}$,AD=2,则BA的长为( )
如图,在△ABC中,已知点D在BC边上,cos∠ADC=$\frac{\sqrt{2}}{3}$,cos∠BAD=$\frac{\sqrt{3}}{3}$,AD=2,则BA的长为( )| A. | $\frac{14\sqrt{3}+4\sqrt{21}}{3}$ | B. | 7$\sqrt{3}$+4 | C. | $\sqrt{3}$+4$\sqrt{7}$ | D. | 7+4$\sqrt{7}$ |
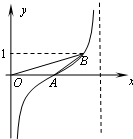
| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{9}{2}$ |
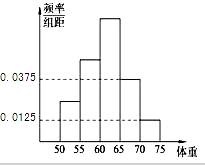 某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.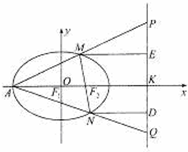 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.