题目内容
13.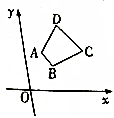 已知梯形ABCD,如图所示,其中AB∥CD,且DC=2AB,三个顶点的坐标分别为A(1,2)、B(2,1)、C(4,2),求点D的坐标.
已知梯形ABCD,如图所示,其中AB∥CD,且DC=2AB,三个顶点的坐标分别为A(1,2)、B(2,1)、C(4,2),求点D的坐标.
分析 设出点D的坐标,用坐标表示写出$\overrightarrow{AB}$、$\overrightarrow{DC}$,由向量平行与相等,列出方程组,求出点D的坐标.
解答 解:设点D的坐标为(x,y),
∴$\overrightarrow{AB}$=(2-1,1-2)=(1,-1),
$\overrightarrow{DC}$=(4-x,2-y);
∵AB∥CD,∴$\overrightarrow{AB}$∥$\overrightarrow{DC}$,
即1•(2-y)-(-1)•(4-x)=0,①
又∵DC=2AB,∴$\overrightarrow{DC}$=2$\overrightarrow{AC}$,
即(4-x,2-y)=2(1,-1),
∴$\left\{\begin{array}{l}{4-x=2}\\{2-y=-2}\end{array}\right.$;②
由①、②组成方程组,
解得x=2,y=4,
∴点D的坐标为(2,4).
点评 本题考查了平面向量的坐标表示与应用问题,也考查了向量相等与平行的坐标表示问题,考查了方程组的解法与应用问题,是基础题目.

练习册系列答案
相关题目
18.函数y=tan($\frac{π}{4}x-\frac{π}{2}$)的部分图象如图所示,则△AOB的面积等于( )
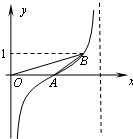

| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{9}{2}$ |
 如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.
如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别是F1(-c,0),F2(c,0),直线l:x=my-c与椭圆C交于点M,N两点,当m=-$\frac{{\sqrt{3}}}{3}$,M是椭圆C的顶点,且△MF1F2的周长为6.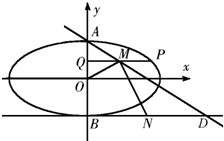 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.