题目内容
10.已知函数f(x)=lnx-m(x-1).若函数f(x)在点[$\frac{1}{2}$,f($\frac{1}{2}$)]处的切线与直线y+x+1=0相互垂直.(1)求m的值.
(2)求函数f(x)的最大值.
分析 (1)求导数,确定切线的斜率,利用函数f(x)在点[$\frac{1}{2}$,f($\frac{1}{2}$)]处的切线与直线y+x+1=0相互垂直,建立方程,即可求m的值.
(2)确定函数在(0,1)上单调递增,在(1,+∞)上单调递减,即可求函数f(x)的最大值.
解答 解:(1)因为f(x)=lnx-m(x-1),
所以f′(x)=$\frac{1}{x}$-m,
所以f′($\frac{1}{2}$)=2-m,
因为函数f(x)在点[$\frac{1}{2}$,f($\frac{1}{2}$)]处的切线与直线y+x+1=0相互垂直,
所以2-m=1,
所以m=1;
(2)f(x)=lnx-(x-1),f′(x)=$\frac{1}{x}$-1,
所以0<x<1时,f′(x)>0,x>1时,f′(x)<0,
所以函数在(0,1)上单调递增,在(1,+∞)上单调递减,
所以x=1时,函数f(x)的最大值为0.
点评 本题考查导数的综合运用,考查导数的几何意义,考查函数的单调性与最大值,正确求出导数是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.函数y=tan($\frac{π}{4}x-\frac{π}{2}$)的部分图象如图所示,则△AOB的面积等于( )
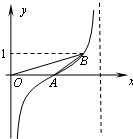

| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{9}{2}$ |
15.已知z为复数,(1-i)2z=(1+i)3(i为虚数单位),则$\overline z$=( )
| A. | 1+i | B. | -1+i | C. | 1-i | D. | -1-i |
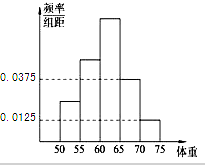 某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.