题目内容
7.计算:$\frac{4}{1×3}$-$\frac{8}{3×5}$+$\frac{12}{5×7}$-$\frac{16}{7×9}$+…+(-1)n+1$\frac{4n}{(2n-1)(2n+1)}$=$\left\{\begin{array}{l}1+\frac{1}{2n+1},n为奇数\\ 1-\frac{1}{2n+1},n为偶数\end{array}\right.$.分析 通过裂项法,利用n为奇数与偶数,分别求解数列的和即可.
解答 解:因为$\frac{4n}{(2n-1)(2n+1)}$=$\frac{1}{2n-1}+\frac{1}{2n+1}$,
所以当n为奇数时,
$\frac{4}{1×3}$-$\frac{8}{3×5}$+$\frac{12}{5×7}$-$\frac{16}{7×9}$+…+(-1)n+1$\frac{4n}{(2n-1)(2n+1)}$
=$1+\frac{1}{3}$$-\frac{1}{3}-\frac{1}{5}$$+\frac{1}{5}+\frac{1}{7}$-…$-\frac{1}{2n-3}-\frac{1}{2n-1}$$+\frac{1}{2n-1}+\frac{1}{2n+1}$
=1+$\frac{1}{2n+1}$.
当n为偶数时,
$\frac{4}{1×3}$-$\frac{8}{3×5}$+$\frac{12}{5×7}$-$\frac{16}{7×9}$+…+(-1)n+1$\frac{4n}{(2n-1)(2n+1)}$
=$1+\frac{1}{3}$$-\frac{1}{3}-\frac{1}{5}$$+\frac{1}{5}+\frac{1}{7}$-…$+\frac{1}{2n-3}+\frac{1}{2n-1}$$-\frac{1}{2n-1}-\frac{1}{2n+1}$
=1-$\frac{1}{2n+1}$.
故答案为:$\left\{\begin{array}{l}1+\frac{1}{2n+1},n为奇数\\ 1-\frac{1}{2n+1},n为偶数\end{array}\right.$.
点评 本题考查数列求和,裂项法的应用,考查分类讨论的应用.

 已知圆F1:(x+1)2+y2=8,点F2(1,0),点Q在圆F1上运动,QF2的垂直平分线交QF1于点P.
已知圆F1:(x+1)2+y2=8,点F2(1,0),点Q在圆F1上运动,QF2的垂直平分线交QF1于点P. 如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.
如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.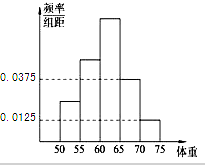 某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.