题目内容
13.设A(0,3),B(3,3),C(2,0),直线x=a将△ABC分割成面积相等的两部分,求a的值.分析 求出AC所在的直线方程,再联立方程x=a求出E点的坐标,进而得出DE和AD的长,再由三角形的面积即可得出a的值.
解答 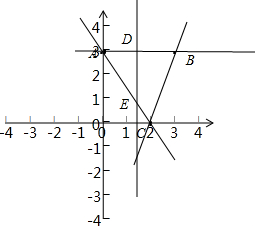 解:AC所在的直线方程为y=-$\frac{3}{2}$x+3,
解:AC所在的直线方程为y=-$\frac{3}{2}$x+3,
直线x=a与AB交于D,与AC交于E,
则S△ADE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{3×3}{2}$=$\frac{9}{4}$,
E点的坐标为﹙a,-$\frac{3a}{2}$+3﹚,
∴DE=3-﹙-$\frac{3a}{2}$+3﹚=$\frac{3a}{2}$,
AD=a,∴由S△ADE=$\frac{AD•DE}{2}$=$\frac{1}{2}$×a•$\frac{3a}{2}$=$\frac{9}{4}$,
解得:a=$\sqrt{3}$.
点评 此题考查了两直线的交点坐标,求出S△ADE是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.PM 2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准GB3095-2012,PM 2.5日均值在35微克/立方米以下,空气质量为一级;在35微克/立方米~75微克/立方米之间,空气质量为二级;在75微克/立方米以上,空气质量为超标.从某自然保护区2014年全年每天的PM 2.5监测数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
(1)从这10天的PM 2.5日均值监测数据中,随机抽出3天,求恰有一天空气质量达到一级的概率;
(2)从这10天的数据中任取3天数据,记ξ表示抽到PM 2.5监测数据超标的天数,求ξ的分布列;
(3)以这10天的PM 2.5日均值来估计一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级(精确到整数).
| PM 2.5日均值(微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
(2)从这10天的数据中任取3天数据,记ξ表示抽到PM 2.5监测数据超标的天数,求ξ的分布列;
(3)以这10天的PM 2.5日均值来估计一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级(精确到整数).
2.F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的右焦点,点P在双曲线右支上,△POF(O为坐标原点)是面积为$\sqrt{3}$的等边三角形,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$+1 |
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,右顶点为(2,0),离心率为$\frac{{\sqrt{3}}}{2}$,直线l1:y=kx+m(k≠0,m≠0)与椭圆C相交于不同的两点A,B,过AB的中点M作垂直于l1的直线l2,设l2与椭圆C相交于不同的两点C,D,且CD的中点为N.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,右顶点为(2,0),离心率为$\frac{{\sqrt{3}}}{2}$,直线l1:y=kx+m(k≠0,m≠0)与椭圆C相交于不同的两点A,B,过AB的中点M作垂直于l1的直线l2,设l2与椭圆C相交于不同的两点C,D,且CD的中点为N.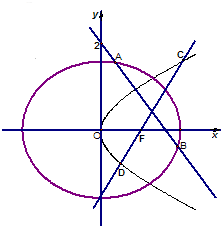 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同. 如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1.
如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1.