题目内容
8. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为$\frac{1}{2}$,椭圆C的右焦点F和抛物线G:y2=4x的焦点相同.(1)求椭圆C的方程.
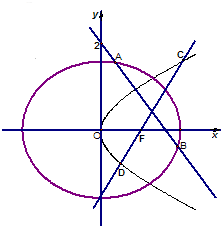
(2)如图,已知直线l:y=kx+2与椭圆C及抛物线G都有两个不同的公共点,且直线l与椭圆C交于A,B两点;过焦点F的直线l′与抛物线G交于C,D两点,记$λ=\overrightarrow{OA}•\overrightarrow{OB}-\overrightarrow{OC}•\overrightarrow{OD}$,求λ的取值范围.
分析 (1)运用离心率公式和抛物线的焦点,以及a,b,c的关系,即可得到椭圆的方程;
(2)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),联立直线方程和椭圆方程,以及直线方程和抛物线方程运用韦达定理和判别式大于0,结合向量的数量积的坐标表示,解不等式即可得到所求范围.
解答 解:(1)椭圆的离心率$\frac{c}{a}=\frac{1}{2}$,抛物线y2=4x的焦点为(1,0),
所以椭圆中的c=1,a=2,b2=3.所以椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(2)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),则
由$\left\{{\begin{array}{l}{\frac{x^2}{4}+\frac{y^2}{3}=1}\\{y=kx+2}\end{array}}\right.$,消去y可得(3+4k2)x2+16kx+4=0(①),
由${△_1}={(16k)^2}-4×4×(3+4{k^2})>0$解得$k<-\frac{1}{2}$或$k>\frac{1}{2}$;
由$\left\{{\begin{array}{l}{{y^2}=4x}\\{y=kx+2}\end{array}}\right.$消去y可得k2x2+4(k-1)x+4=0,
由${△_2}=16{(k-1)^2}-16{k^2}>0$
解得$k<\frac{1}{2}$,所以$k<-\frac{1}{2}$.
由①可得$\left\{{\begin{array}{l}{{x_1}+{x_2}=-\frac{16k}{{3+4{k^2}}}}\\{{x_1}•{x_2}=\frac{4}{{3+4{k^2}}}}\end{array}}\right.$,
y1•y2=(kx1+2)•(kx2+2)=k2x1•x2+2k(x1+x2)+4=$\frac{{12-12{k^2}}}{{3+4{k^2}}}$,
所以$\overrightarrow{OA}•\overrightarrow{OB}={x_1}{x_2}+{y_1}{y_2}=\frac{{16-12{k^2}}}{{3+4{k^2}}}$,
当l'的斜率不存在时,C(1,2),D(1,-2),此时,$\overrightarrow{OC}•\overrightarrow{OD}=-3$;
当l'的斜率存在时,设l'的方程为y=m(x-1),(m≠0),
由$\left\{{\begin{array}{l}{{y^2}=4x}\\{y=m(x-1)}\end{array}}\right.$消去y可得m2x2-(2m2+4)x+m2=0,
所以x3•x4=1,${y_3}{y_4}=-4\sqrt{{x_1}{x_2}}=-4$,
所以$\overrightarrow{OC}•\overrightarrow{OD}=-3$,
则λ=$\frac{{16-12{k^2}}}{{3+4{k^2}}}+3$=$\frac{25}{{3+4{k^2}}}$,
因为$k<-\frac{1}{2}$,所以${k^2}>\frac{1}{4}$,
所以$0<λ<\frac{25}{4}$.
点评 本题考查椭圆和抛物线的方程和性质,主要考查椭圆的离心率和抛物线的焦点,同时考查直线和椭圆方程联立,直线和抛物线方程联立,运用韦达定理,以及向量的数量积的坐标表示,考查运算能力,属于中档题和易错题.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | -$\frac{1}{π}$ | B. | 1-$\frac{2}{π}$ | C. | $\frac{1}{π}$ | D. | $\frac{2}{π}$ |
 如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,若AB=2PC=$\sqrt{2}$,D是PC的中点
如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,若AB=2PC=$\sqrt{2}$,D是PC的中点