题目内容
2.F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的右焦点,点P在双曲线右支上,△POF(O为坐标原点)是面积为$\sqrt{3}$的等边三角形,则双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$+1 |
分析 利用双曲线的性质、正三角形的性质和面积公式和离心率的公式即可得出.
解答 解:由△POF是面积为$\sqrt{3}$的等边三角形,
即$\sqrt{3}$=$\frac{\sqrt{3}}{4}$c2,解得c=2.
又线段OF的中点M的横坐标为$\frac{1}{2}$c=1,
即为点P的横坐标,即有P(1,±$\sqrt{3}$),
代入双曲线的方程得$\frac{1}{{a}^{2}}$-$\frac{3}{{b}^{2}}$=1,
又a2+b2=4,
解得a=$\sqrt{3}±1$,由c>a,可得a=$\sqrt{3}-1$,
则e=$\frac{c}{a}$=$\sqrt{3}+1$.
故选:D.
点评 熟练掌握双曲线的性质、正三角形的性质和面积公式是解题的关键.

练习册系列答案
相关题目
10.某设备的使用年限x(单位:年)与所支付的维修费用y(单位:千元)的一组数据如表:
从散点图分析.Y与x线性相关,根据上表中数据可得其线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{b}$=1.54.由此预测该设备的使用年限为6年时需支付的维修费用约是( )
| 使用年限x | 2 | 3 | 4 | 5 |
| 维修费用y | 2 | 3.4 | 5 | 6.6 |
| A. | 7.2千元 | B. | 7.8千元 | C. | 8.1千元 | D. | 9.5千元 |
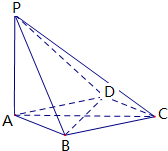 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的菱形,且∠BAD=60°,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的菱形,且∠BAD=60°,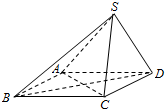 已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.
已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.