题目内容
3. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,右顶点为(2,0),离心率为$\frac{{\sqrt{3}}}{2}$,直线l1:y=kx+m(k≠0,m≠0)与椭圆C相交于不同的两点A,B,过AB的中点M作垂直于l1的直线l2,设l2与椭圆C相交于不同的两点C,D,且CD的中点为N.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,右顶点为(2,0),离心率为$\frac{{\sqrt{3}}}{2}$,直线l1:y=kx+m(k≠0,m≠0)与椭圆C相交于不同的两点A,B,过AB的中点M作垂直于l1的直线l2,设l2与椭圆C相交于不同的两点C,D,且CD的中点为N.(Ⅰ)求椭圆C的方程;
(Ⅱ)设原点O到直线l1的距离为d,求$\frac{{|{MN}|}}{d}$的取值范围.
分析 (Ⅰ)运用离心率公式和a,b,c的关系,解得a,b,进而得到椭圆方程;
(Ⅱ)设出AB的方程,代入椭圆方程,运用韦达定理,可得中点的坐标,再设直线CD的方程,代入椭圆方程,运用韦达定理和弦长公式和点到直线的距离公式,再由二次函数的最值,即可得到范围.
解答 解:(Ⅰ)由$\left\{\begin{array}{l}a=2\\ \frac{c}{a}=\frac{{\sqrt{3}}}{2}\end{array}\right.$得a=2,c=$\sqrt{3}$,
b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
则椭圆方程为$\frac{x^2}{4}+{y^2}=1$;
(Ⅱ)由$\left\{\begin{array}{l}\frac{x^2}{4}+{y^2}=1\\ y=kx+m\end{array}\right.$得(1+4k2)x2+8kmx+4m2-4=0,
设A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}{x_1}+{x_2}=-\frac{8mk}{{1+4{k^2}}}\\{x_1}{x_2}=\frac{{4{m^2}-4}}{{1+4{k^2}}}.\end{array}\right.$,
故$M(-\frac{4mk}{{1+4{k^2}}},\frac{m}{{1+4{k^2}}})$,
l2:y-$\frac{m}{1+4{k}^{2}}$=-$\frac{1}{k}$(x+$\frac{4mk}{1+4{k}^{2}}$),即$y=-\frac{1}{k}x-\frac{3m}{{1+4{k^2}}}$,
由$\left\{\begin{array}{l}y=-\frac{1}{k}x-\frac{3m}{{1+4{k^2}}}\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$,得$(1+\frac{4}{k^2}){x^2}+\frac{24m}{{k(1+4{k^2})}}x+\frac{{36{m^2}}}{{{{(1+4{k^2})}^2}}}-4=0$,
设C(x3,y3),D(x4,y4),
则${x_3}+{x_4}=-\frac{24mk}{{(1+4{k^2})({k^2}+4)}}$,
故$N(-\frac{12mk}{{(1+4{k^2})({k^2}+4)}},-\frac{{3m{k^2}}}{{(1+4{k^2})({k^2}+4)}})$,
故$|{MN}|=|{x_M}-{x_N}|\sqrt{1+\frac{1}{k^2}}$=$\frac{{4|m|({k^2}+1)\sqrt{{k^2}+1}}}{{(1+4{k^2})({k^2}+4)}}$,
又$d=\frac{|m|}{{\sqrt{1+{k^2}}}}$,
所以$\frac{{|{MN}|}}{d}$=$\frac{{4{{({k^2}+1)}^2}}}{{(1+4{k^2})({k^2}+4)}}$.
令t=k2+1(t>1),
则$\frac{{|{MN}|}}{d}$=$\frac{{4{t^2}}}{{4{t^2}+9t-9}}=\frac{4}{{-\frac{9}{t^2}+\frac{9}{t}+4}}=\frac{4}{{-9{{(\frac{1}{t}-\frac{1}{2})}^2}+\frac{25}{4}}}$$∈[\frac{16}{25},1)$.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,联立直线方程和椭圆方程,运用韦达定理和弦长公式,同时考查两直线的位置关系,考查运算能力,属于中档题.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
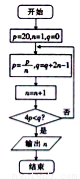
ABC考王全优卷系列答案 的值是( )
的值是( )