题目内容
3.已知函数f(x)=aln(1+x)-aln(1-x)-x-$\frac{x^3}{{3(1-{x^2})}}$.(1)当0<x<1时,f(x)<0,求实数a的取值范围;
(2)证明:$\frac{3}{2}$ln2+$\frac{5}{2}$ln$\frac{3}{2}$+…+(n+$\frac{1}{2}$)ln$\frac{n+1}{n}$<n+$\frac{1}{12}$•$\frac{n}{(n+1)}$(n∈N*).
分析 (1)求导数,利用判别式分类讨论,结合函数的单调性,即可求实数a的取值范围;
(2)先确定$\frac{1}{2}$ln$\frac{n+1}{n}$-$\frac{1}{2n+1}$<$\frac{1}{12(2n+1)({n}^{2}+n)}$,裂项累加可得结论.
解答 (1)解:f′(x)=$\frac{-2{x}^{4}+(3-6a){x}^{2}+6a-3}{3(1-{x}^{2})^{2}}$,…(1分)
依题知f(0)=0,故f′(x)≤0,则a≤$\frac{1}{2}$.…(2分)
令g(x)=-2x2+(3-6a)x+6a-3,x∈(0,1],△=(6a-3)(6a+5)
①-$\frac{5}{6}$$≤a≤\frac{1}{2}$,△≤0,此时g(x)≤0,故f′(x)≤0,而f(0)=0,所以-$\frac{5}{6}$$≤a≤\frac{1}{2}$符合题意.…(4分)
②a<-$\frac{5}{6}$,△>0,而g(x)对称轴x=$\frac{3-6a}{4}$>2,故g(x)在(0,1)单调递增且g(1)=-2,则g(x)<0,故f′(x)≤0,而f(0)=0,所以a<-$\frac{5}{6}$符合题意.…(6分)
综上,a≤$\frac{1}{2}$.…(7分)
(2)证明:由(1)知,当a=$\frac{1}{2}$,0<x<1时,f(x)<0,
即$\frac{1}{2}$ln$\frac{1+x}{1-x}$-x<$\frac{{x}^{3}}{3(1-{x}^{2})}$.…(8分)
令x=$\frac{1}{2n+1}$(n∈N*),则$\frac{1}{2}$ln$\frac{n+1}{n}$-$\frac{1}{2n+1}$<$\frac{1}{12(2n+1)({n}^{2}+n)}$,(10分)
裂项累加(n+$\frac{1}{2}$)ln$\frac{n+1}{n}$-1<$\frac{1}{12}$($\frac{1}{n}$-$\frac{1}{n+1}$)
所以$\frac{3}{2}$ln2+$\frac{5}{2}$ln$\frac{3}{2}$+…+(n+$\frac{1}{2}$)ln$\frac{n+1}{n}$<n+$\frac{1}{12}$•$\frac{n}{(n+1)}$.(12分)
点评 本题考查导数知识的综合运用,考查函数的单调性,考查不等式的证明,正确运用导数的关键.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案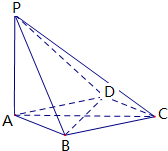 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的菱形,且∠BAD=60°,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的菱形,且∠BAD=60°,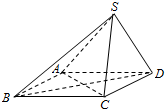 已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.
已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.