题目内容
已知函数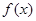 是定义在
是定义在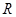 上的奇函数,当
上的奇函数,当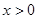 时,
时,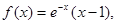 给出以下命题:
给出以下命题:
①当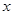
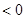 时,
时,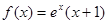 ; ②函数
; ②函数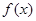 有五个零点;
有五个零点;
③对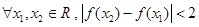 恒成立.
恒成立.
④若关于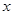 的方程
的方程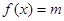 有解,则实数
有解,则实数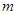 的取值范围是
的取值范围是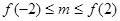 ;
;
其中,正确命题的序号是 .
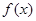 是定义在
是定义在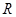 上的奇函数,当
上的奇函数,当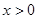 时,
时,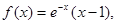 给出以下命题:
给出以下命题:①当
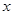
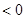 时,
时,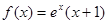 ; ②函数
; ②函数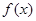 有五个零点;
有五个零点;③对
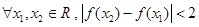 恒成立.
恒成立.④若关于
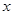 的方程
的方程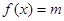 有解,则实数
有解,则实数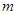 的取值范围是
的取值范围是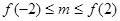 ;
;其中,正确命题的序号是 .
①③
试题分析:由
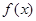 为
为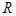 上的奇函数,
上的奇函数,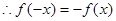 ,
,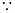 当
当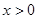 时,
时,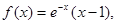
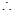 当
当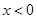 时,
时,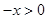 ,
,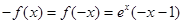 ,即
,即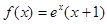 ,故①正确;对
,故①正确;对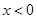 时的解析式求导数可得,
时的解析式求导数可得,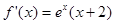 ,令
,令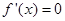 ,解得
,解得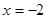 ,且当
,且当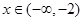 时,
时,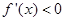 ,函数单调递减;当
,函数单调递减;当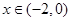 时,
时,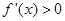 ,函数单调递增;
,函数单调递增;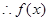 的极小值为
的极小值为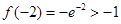 ,又
,又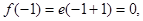 而当
而当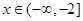 时,
时,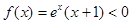 恒成立,又因为奇函数的图象关于原点对称,故函数
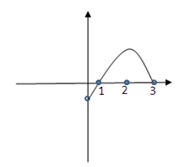
恒成立,又因为奇函数的图象关于原点对称,故函数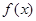 的大致图象应如图所示:
的大致图象应如图所示: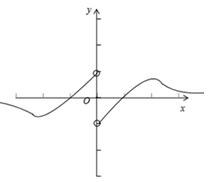
由图象易知,函数
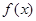 有3个零点,即②错误;由图知
有3个零点,即②错误;由图知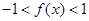 ,
,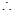 对
对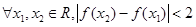 恒成立,即③正确;若关于方程
恒成立,即③正确;若关于方程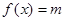 有解,则实数
有解,则实数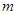 的取值范围为
的取值范围为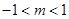 ,故④错.
,故④错.故答案为①③.

练习册系列答案
相关题目
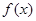 是定义在R上的奇函数,当
是定义在R上的奇函数,当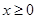 时
时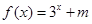 (m为常数),则
(m为常数),则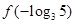 的值为( ).
的值为( ).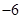
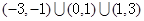
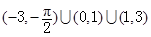
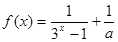 是奇函数,则
是奇函数,则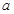 的值为( )
的值为( )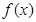 满足
满足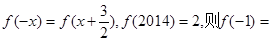 .
.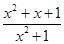 ,若f(a)=
,若f(a)=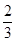 ,则f(-a)=________.
,则f(-a)=________.