题目内容
已知函数f(x)=x2+2ax+2,x∈[-5,5],
(1)当a=1时,求f(x)的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数.
(1)当a=1时,求f(x)的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数.
(1)f(x)=x2+2ax+2=(x+a)2+2-a2,
其对称轴为x=-a,当a=1时,f(x)=x2+2x+2,
所以当x=-1时,f(x)min=f(-1)=1-2+2=1;
当x=5时,即当a=1时,f(x)的最大值是37,最小值是1.(6分)
(2)当区间[-5,5]在对称轴的一侧时,
函数y=f(x)是单调函数.所以-a≤-5或-a≥5,
即a≥5或a≤-5,即实数a的取值范围是(-∞,-5]∪[5,+∞)时,
函数在区间[-5,5]上为单调函数.(12分)
其对称轴为x=-a,当a=1时,f(x)=x2+2x+2,
所以当x=-1时,f(x)min=f(-1)=1-2+2=1;
当x=5时,即当a=1时,f(x)的最大值是37,最小值是1.(6分)
(2)当区间[-5,5]在对称轴的一侧时,
函数y=f(x)是单调函数.所以-a≤-5或-a≥5,
即a≥5或a≤-5,即实数a的取值范围是(-∞,-5]∪[5,+∞)时,
函数在区间[-5,5]上为单调函数.(12分)

练习册系列答案
相关题目
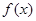 是定义在
是定义在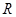 上的奇函数,当
上的奇函数,当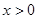 时,
时,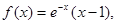 给出以下命题:
给出以下命题: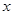
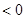 时,
时,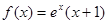 ; ②函数
; ②函数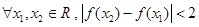 恒成立.
恒成立.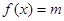 有解,则实数
有解,则实数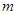 的取值范围是
的取值范围是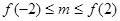 ;
;