题目内容
【题目】已知函数![]() 的图象与
的图象与![]() 轴相切,且切点在
轴相切,且切点在![]() 轴的正半轴上.
轴的正半轴上.
(1)求曲线![]() 与
与![]() 轴,直线
轴,直线![]() 及
及![]() 轴围成图形的面积
轴围成图形的面积![]() ;
;
(2)若函数![]() 在
在![]() 上的极小值不大于
上的极小值不大于![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据导数的几何意义可得到![]() 得
得![]() ,
, ![]() ,解得
,解得![]() .(2)先求导
.(2)先求导![]() ,研究导函数的正负,当
,研究导函数的正负,当![]() 时,
时, ![]() 无极值;当
无极值;当![]() ,即
,即![]() 时,分析导数的正负使得极值
时,分析导数的正负使得极值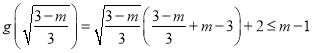 ,解出不等式即可。
,解出不等式即可。
解:(1)![]() ,
, ![]() 得
得![]() ,
,
由题意可得![]() ,解得
,解得![]() .
.
故![]() ,
, 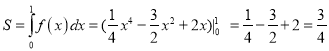 .
.
(2)![]() ,
, ![]()
当![]() 时,
时, ![]() 无极值;
无极值;
当![]() ,即
,即![]() 时,令
时,令![]() 得
得![]() ;
;
令![]() 得
得![]() 或.
或. ![]()
![]() 在
在![]() 处取得极小值,
处取得极小值,
当![]() ,即
,即![]() ,
, ![]() 在(-3,2)上无极小值,
在(-3,2)上无极小值,
故当![]() 时,
时, ![]() 在(-3,2)上有极小值
在(-3,2)上有极小值
且极小值为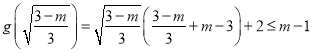 ,
,
即![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
又![]() ,故
,故![]() .
.
点睛:这个题目考查的是利用导数研究函数的极值;求导后出现二次函数形式,一般的讨论方法有:先看二次项系数是否为0,然后看能否因式分解,能分解的话,直接比较两根的大小,不能分解就由判别式和图像结合判断导函数的正负。

练习册系列答案
相关题目