题目内容
【题目】已知f（x）=sin（x+1） 
﹣ 
cos（x+1） ，则f（1）+f（2）+f（3）+…+f（2011）=（ ）
A.2
B.
C.﹣
D.0
【答案】B
【解析】解：∵f（x）=sin（x+1） 
﹣ 
cos（x+1） ，
=sin（ 
+ ）﹣ cos（ + ）
=2sin（ + ﹣ ）
=2sin ，
∴函数f（x）的周期T= 
=6，
又f（1）+f（2）+f（3）+f（4）+f（5）+f（6）=0，
且2011=335×6+1，
故f（1）+f（2）+f（3）+…+f（2011）=335×0+f（1）=f（1）=2sin = ．
故选：B．
【考点精析】认真审题，首先需要了解函数的值(函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法)．
练习册系列答案
名校课堂系列答案
相关题目
【题目】给出最小二乘法下的回归直线方程 
= 
x+ 
系数公式： = 
， 
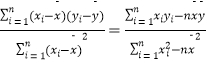假设关于某设备的使用年限x（年）和所支出的维修费用y（万元），有如表的统计资料：
使用年限x （年） | 2 | 3 | 4 | 5 | 6 |
维修费用y（万元） | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料可知y对x呈线性相关关系，试求：
（1）线性回归直线方程；
（2）根据回归直线方程，估计使用年限为12年时，维修费用是多少？
