题目内容
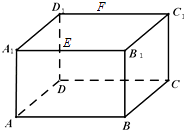
【题目】如图,M是正方体ABCD﹣A1B1C1D1的棱DD1的中点,给出下列命题
①过M点有且只有一条直线与直线AB、B1C1都相交;
②过M点有且只有一条直线与直线AB、B1C1都垂直;
③过M点有且只有一个平面与直线AB、B1C1都相交;
④过M点有且只有一个平面与直线AB、B1C1都平行.
其中真命题是( )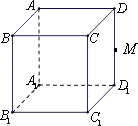
A.②③④
B.①③④
C.①②④
D.①②③
【答案】C
【解析】解:直线AB与B1C1 是两条互相垂直的异面直线,点M不在这两异面直线中的任何一条上,如图所示:
取C1C的中点N,则MN∥AB,且 MN=AB,设BN 与B1C1交于H,则点 A、B、M、N、H 共面,
直线HM必与AB直线相交于某点O.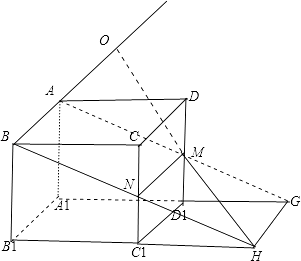
所以,过M点有且只有一条直线HO与直线AB、B1C1都相交;故①正确.
过M点有且只有一条直线与直线AB、B1C1都垂直,此垂线就是棱DD1 , 故②正确.
过M点有无数个平面与直线AB、B1C1都相交,故 ③不正确.
过M点有且只有一个平面与直线AB、B1C1都平行,此平面就是过M点与正方体的上下底都平行的平面,故④正确.
综上,①②④正确,③不正确,
故选 C.
【考点精析】认真审题,首先需要了解直线与平面平行的性质(一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行),还要掌握平面与平面垂直的性质(两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直)的相关知识才是答题的关键.

【题目】给出最小二乘法下的回归直线方程 ![]() =
= ![]() x+
x+ ![]() 系数公式:
系数公式: ![]() =
= 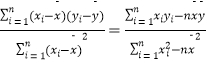 ,
, ![]()
假设关于某设备的使用年限x(年)和所支出的维修费用y(万元),有如表的统计资料:
使用年限x (年) | 2 | 3 | 4 | 5 | 6 |
维修费用y(万元) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料可知y对x呈线性相关关系,试求:
(1)线性回归直线方程;
(2)根据回归直线方程,估计使用年限为12年时,维修费用是多少?