题目内容
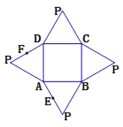
【题目】如图是一个几何体的平面展开图,其中四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,
,![]() ,
,![]() 为全等的等边三角形,
为全等的等边三角形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,在此几何体中,下列结论中正确的个数有()
的中点,在此几何体中,下列结论中正确的个数有()
①平面![]() 平面
平面![]()
②直线![]() 与直线
与直线![]() 是异面直线
是异面直线
③直线![]() 与直线
与直线![]() 共面
共面
④面![]() 与面
与面![]() 的交线与
的交线与![]() 平行
平行
A. 3B. 2C. 1D. 0
【答案】A
【解析】
根据展开图,复原几何体,利用异面直线的定义可以判断出②③的正误,利用面面垂直的判定定理判断①的正误,利用面面平行的性质定理判断④的正误,最后选出正确答案.
根据展开图,复原几何体,如下图所示:

由已知条件,在平面![]() 内,过点
内,过点![]() 的中线垂直于
的中线垂直于![]() ,再也找不到和平面
,再也找不到和平面![]() 内垂直的线段,因此找不到和平面
内垂直的线段,因此找不到和平面![]() 垂直的垂线,由已知四边形
垂直的垂线,由已知四边形![]() 为正方形,能得到
为正方形,能得到![]() 或
或![]() ,再也找不到和平面
,再也找不到和平面![]() 内相垂直的的线段,因此找不到和平面
内相垂直的的线段,因此找不到和平面![]() 垂直的线段,所以不能判断平面
垂直的线段,所以不能判断平面![]() 平面
平面![]() ,故①是不正确的;
,故①是不正确的;
根据异面直线的定义可以判断②是正确的;
因为![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,所以
的中点,所以![]() ,而四边形
,而四边形![]() 为正方形,所以有
为正方形,所以有![]() ,因此有
,因此有![]() ,所以
,所以![]() 中点共面,所以③是正确的;
中点共面,所以③是正确的;
因为![]() ,
,![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以面
,所以面![]() 与面
与面![]() 的交线与
的交线与![]() 平行,故④正确,故有三个结论是正确的,本题选A.
平行,故④正确,故有三个结论是正确的,本题选A.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
【题目】某理财公司有两种理财产品A和B,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品A
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概率 |
|
|
|
产品B
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概率 | p |
| q |
注:p>0,q>0
(1)已知甲、乙两人分别选择了产品A和产品B投资,如果一年后他们中至少有一人获利的概率大于![]() ,求实数p的取值范围;
,求实数p的取值范围;
(2)若丙要将家中闲置的10万元人民币进行投资,以一年后投资收益的期望值为决策依据,则选用哪种产品投资较理想?
