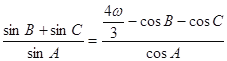ћвƒњƒЏ»Ё
°Њћвƒњ°њƒ≥јн≤∆єЂЋЊ”–Ѕљ÷÷јн≤∆≤ъ∆ЈAЇЌB£ђ’вЅљ÷÷јн≤∆≤ъ∆Ј“їƒкЇу”ѓњчµƒ«йњц»зѕ¬£®√њ÷÷јн≤∆≤ъ∆Јµƒ≤їЌђЌґ„ љбєы÷ЃЉдѕаї•ґјЅҐ£©£Ї
≤ъ∆ЈA
Ќґ„ љбєы | їсјы40% | ≤ї≈в≤ї„ђ | њчЋр20% |
Є≈¬ |
|
|
|
≤ъ∆ЈB
Ќґ„ љбєы | їсјы20% | ≤ї≈в≤ї„ђ | њчЋр10% |
Є≈¬ | p |
| q |
„Ґ£Їp£Њ0£ђq£Њ0
£®1£©“—÷™Љ„°Ґ““Ѕљ»ЋЈ÷±р—°‘сЅЋ≤ъ∆ЈAЇЌ≤ъ∆ЈBЌґ„ £ђ»зєы“їƒкЇуЋы√«÷–÷Ѕ…ў”–“ї»ЋїсјыµƒЄ≈¬ іу”Џ![]() £ђ«у µ эpµƒ»°÷µЈґќІ£ї
£ђ«у µ эpµƒ»°÷µЈґќІ£ї
£®2£©»ф±ы“™љЂЉ“÷–ѕ–÷√µƒ10Ќт‘™»Ћ√с±“љш––Ќґ„ £ђ“‘“їƒкЇуЌґ„ ’“жµƒ∆ЏЌы÷µќ™Њц≤я“јЊЁ£ђ‘т—°”√ƒƒ÷÷≤ъ∆ЈЌґ„ љѕјнѕл£њ
°Њір∞Є°њ£®1£©![]() £ї
£ї
£®2£©µ±![]() ±£ђE(X)£љE(Y)£ђ—°‘с≤ъ∆ЈAЇЌ≤ъ∆ЈB“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыѕаЌђ£ђњ…“‘‘Џ≤ъ∆ЈAЇЌ≤ъ∆ЈB÷–»ќ—°“їЄц£ї
±£ђE(X)£љE(Y)£ђ—°‘с≤ъ∆ЈAЇЌ≤ъ∆ЈB“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыѕаЌђ£ђњ…“‘‘Џ≤ъ∆ЈAЇЌ≤ъ∆ЈB÷–»ќ—°“їЄц£ї
µ±![]() ±£ђE(X)£ЊE(Y)£ђ—°‘с≤ъ∆ЈA“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыљѕіу£ђ”¶—°≤ъ∆ЈA£ї
±£ђE(X)£ЊE(Y)£ђ—°‘с≤ъ∆ЈA“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыљѕіу£ђ”¶—°≤ъ∆ЈA£ї
µ±![]() ±£ђE(X)£ЉE(Y)£ђ—°‘с≤ъ∆ЈB“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыљѕіу£ђ”¶—°≤ъ∆ЈB£Ѓ
±£ђE(X)£ЉE(Y)£ђ—°‘с≤ъ∆ЈB“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыљѕіу£ђ”¶—°≤ъ∆ЈB£Ѓ
°Њљвќц°њ
£®1£©ѕ»±н Њ≥цЅљ»Ћ»ЂґЉ≤їїсјыµƒЄ≈¬ £ђ‘ў«у÷Ѕ…ў”–“ї»ЋїсјыµƒЄ≈¬ £ђЅ–≥ц≤їµ» љ«уљв£ї
£®2£©Ј÷±р«у≥цЅљ÷÷≤ъ∆Јµƒ∆ЏЌы÷µ£ђґ‘∆ЏЌы÷–µƒ≤ќ эљш––Ј÷јаћ÷¬џ£ђµ√≥ц»э÷÷«йњц.
£®1£©Љ« ¬ЉюAќ™°∞Љ„—°‘с≤ъ∆ЈA«“”ѓјы°±£ђ ¬ЉюBќ™°∞““—°‘с≤ъ∆ЈB«“”ѓјы°±£ђ ¬ЉюCќ™°∞“їƒкЇуЉ„£ђ““Ѕљ»Ћ÷–÷Ѕ…ў”–“ї»ЋЌґ„ їсјы°±£ђ‘т![]() £ђ
£ђ![]() £Ѓ
£Ѓ
Ћщ“‘![]() £ђљвµ√
£ђљвµ√![]() £Ѓ
£Ѓ
”÷“тќ™![]() £ђq£Њ0£ђЋщ“‘
£ђq£Њ0£ђЋщ“‘![]() £Ѓ
£Ѓ
Ћщ“‘![]() £Ѓ
£Ѓ
£®2£©Љў…и±ы—°‘с≤ъ∆ЈAљш––Ќґ„ £ђ«“Љ«Xќ™їсјыљрґо£®µ•ќї£ЇЌт‘™£©£ђ‘тЋжїъ±дЅњXµƒЈ÷≤ЉЅ–ќ™
X | 4 | 0 | -2 |
p |
|
|
|
‘т![]() £Ѓ
£Ѓ
Љў…и±ы—°‘с≤ъ∆ЈBљш––Ќґ„ £ђ«“Љ«Yќ™їсјыљрґо£®µ•ќї£ЇЌт‘™£©£ђ‘тЋжїъ±дЅњYµƒЈ÷≤ЉЅ–ќ™
Y | 2 | 0 | -1 |
p | p |
| q |
‘т![]() £Ѓ
£Ѓ
ћ÷¬џ£Ї
µ±![]() ±£ђE(X)£љE(Y)£ђ—°‘с≤ъ∆ЈAЇЌ≤ъ∆ЈB“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыѕаЌђ£ђњ…“‘‘Џ≤ъ∆ЈAЇЌ≤ъ∆ЈB÷–»ќ—°“їЄц£ї
±£ђE(X)£љE(Y)£ђ—°‘с≤ъ∆ЈAЇЌ≤ъ∆ЈB“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыѕаЌђ£ђњ…“‘‘Џ≤ъ∆ЈAЇЌ≤ъ∆ЈB÷–»ќ—°“їЄц£ї
µ±![]() ±£ђE(X)£ЊE(Y)£ђ—°‘с≤ъ∆ЈA“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыљѕіу£ђ”¶—°≤ъ∆ЈA£ї
±£ђE(X)£ЊE(Y)£ђ—°‘с≤ъ∆ЈA“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыљѕіу£ђ”¶—°≤ъ∆ЈA£ї
µ±![]() ±£ђE(X)£ЉE(Y)£ђ—°‘с≤ъ∆ЈB“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыљѕіу£ђ”¶—°≤ъ∆ЈB£Ѓ
±£ђE(X)£ЉE(Y)£ђ—°‘с≤ъ∆ЈB“їƒкЇуЌґ„ ’“жµƒ э—І∆ЏЌыљѕіу£ђ”¶—°≤ъ∆ЈB£Ѓ

°Њћвƒњ°њƒ≥÷–—ІљЂ100√ыЄя“ї–¬…ъЈ÷≥…ЋЃ∆љѕаЌђµƒЉ„°Ґ““ЅљЄц∆љ––∞а£ђ√њ∞а50»Ћ£ђƒ≥љћ ¶≤…”√![]() °Ґ
°Ґ![]() Ѕљ÷÷≤їЌђµƒљћ—Іƒ£ љЈ÷±р‘ЏЉ„°Ґ““ЅљЄц∞аљш––љћЄƒ µ—й£ђќ™ЅЋЅЋљвљћ—І–Ієы£ђ∆Џƒ©њЉ ‘Їу£ђЄ√љћ ¶Ј÷±рі”Ѕљ∞а÷–ЄчЋжїъ≥й»°20√ы—І…ъµƒ≥…Љ®љш––Ќ≥Љ∆£ђ„ч≥цЊ•“ґЌЉ»зЌЉЋщ Њ£ђЉ«≥…Љ®≤їµЌ”Џ90Ј÷ќ™°∞≥…Љ®”≈–г°±.
Ѕљ÷÷≤їЌђµƒљћ—Іƒ£ љЈ÷±р‘ЏЉ„°Ґ““ЅљЄц∞аљш––љћЄƒ µ—й£ђќ™ЅЋЅЋљвљћ—І–Ієы£ђ∆Џƒ©њЉ ‘Їу£ђЄ√љћ ¶Ј÷±рі”Ѕљ∞а÷–ЄчЋжїъ≥й»°20√ы—І…ъµƒ≥…Љ®љш––Ќ≥Љ∆£ђ„ч≥цЊ•“ґЌЉ»зЌЉЋщ Њ£ђЉ«≥…Љ®≤їµЌ”Џ90Ј÷ќ™°∞≥…Љ®”≈–г°±.

£®1£©‘Џ““∞аµƒ20ЄцЄцће÷–£ђі”≤їµЌ”Џ86Ј÷µƒ≥…Љ®÷–Ћжїъ≥й»°2»Ћ£ђ«у≥й≥цµƒЅљЄц»ЋЊщ°∞≥…Љ®”≈–г°±µƒЄ≈¬ £ї
£®2£©”…“‘…ѕЌ≥Љ∆ эЊЁћо–і![]() Ѕ–Ѕ™±н£їƒ№Јс‘ЏЈЄінќуµƒЄ≈¬ ≤ї≥ђєэ0.10µƒ«∞ћбѕ¬»ѕќ™≥…Љ®”≈–г”лљћ—Іƒ£–Ќ”–єЎ.
Ѕ–Ѕ™±н£їƒ№Јс‘ЏЈЄінќуµƒЄ≈¬ ≤ї≥ђєэ0.10µƒ«∞ћбѕ¬»ѕќ™≥…Љ®”≈–г”лљћ—Іƒ£–Ќ”–єЎ.
Љ„∞а£® | ““∞а£® | „№Љ∆ | |
≥…Љ®”≈–г | |||
≥…Љ®≤ї”≈–г | |||
„№Љ∆ |
Єљ£Ї![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.847 | 5.024 |