题目内容
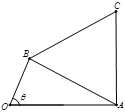
【题目】已知圆心为![]() 的圆过原点
的圆过原点![]() ,且直线
,且直线![]() 与圆
与圆![]() 相切于点
相切于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)已知过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点.
两点.
①若![]() ,求弦
,求弦![]() 的长;
的长;
②若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() 成立,求直线
成立,求直线![]() 的斜率
的斜率![]() .
.
【答案】(1)![]() ;(2)①
;(2)①![]() ,②
,②![]() .
.
【解析】
试题(1)圆心在线段![]() 的垂直平分线上,圆心也在过点
的垂直平分线上,圆心也在过点![]() 且与
且与![]() 垂直的直线上,联立求圆心,进而得半径即可;
垂直的直线上,联立求圆心,进而得半径即可;
(2)①垂径定理即可求弦长;
②圆![]() 上存在点
上存在点![]() ,使得
,使得![]() 成立,即四边形
成立,即四边形![]() 是平行四边形,又
是平行四边形,又![]() ,有
,有![]() 都是等边三角形,进而得圆心
都是等边三角形,进而得圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,列方程求解即可.
,列方程求解即可.
试题解析:
(1)由已知得,圆心在线段![]() 的垂直平分线
的垂直平分线![]() 上,
上,
圆心也在过点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 上,
上,
由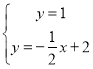 得圆心
得圆心![]() ,
,
所以半径![]() ,
,
所以圆![]() 的方程为
的方程为![]() ;
;
(2)①由题意知,直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
∴圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴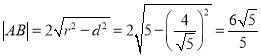 ;
;
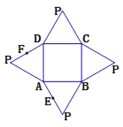
②∵圆![]() 上存在点
上存在点![]() ,使得
,使得![]() 成立,
成立,
∴四边形![]() 是平行四边形,
是平行四边形,
又![]() ,
,
∴![]() 都是等边三角形,
都是等边三角形,
∴圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
又直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
∴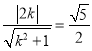 ,
,
解得![]() .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】某中学将100名高一新生分成水平相同的甲、乙两个平行班,每班50人,某教师采用![]() 、
、![]() 两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.
两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.

(1)在乙班的20个个体中,从不低于86分的成绩中随机抽取2人,求抽出的两个人均“成绩优秀”的概率;
(2)由以上统计数据填写![]() 列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
甲班( | 乙班( | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.847 | 5.024 |