题目内容
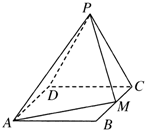
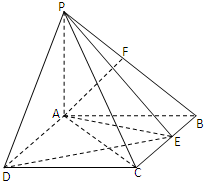
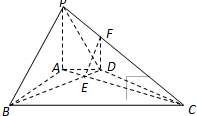
如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=2
,BC=6.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角A-PC-D的余弦值.

| 3 |
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角A-PC-D的余弦值.

解法一:(Ⅰ)∵PA⊥平面ABCD,BD?平面ABCD,∴BD⊥PA.
又tan∠ABD=
=
,tan∠BAC=
=
,
∴∠ABD=30,°∠BAC=60°
∴∠AEB=90°,即BD⊥AC
又PA∩AC=A,
∴BD⊥平面PAC.
(Ⅱ)过E作EF⊥PC,垂足为F,连接DF,
∵DE⊥平面PAC,EF是DF在平面PAC上的射影,由三垂线定理知PC⊥DF,
∴∠EFD为二面角A-PC-D的平面角.
又∠DAC=90°-∠BAC=30°
∴DE=ADsin∠DAC=1,AE=ABsin∠ABE=
,
又AC=4
,
∴EC=3
,PC=8.
由Rt△EFC∽Rt△PAC得EF=
=
在Rt△EFD中,tan∠EFD=
=
,
∴cos∠EFD=
.
∴二面角A-PC-D的余弦值为
.
解法二:(Ⅰ)如图,建立坐标系,则A(0,0,0),B(2
,0,0),C(2
,6,0),D(0,2,0),P(0,0,4)
∴
=(0,0,4),
=(2
,6,0),
=(-2
,2,0)
∴
•
=0,
•
=0,
∴BD⊥AP,BD⊥AC,又PA∩AC=A
∴BD⊥平面PAC.
(Ⅱ)设平面PCD的法向量为
=(x,y,1),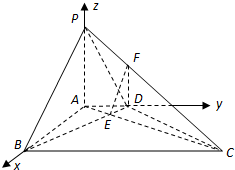
则
•
=0,
•
=0,
又
=(-2
,-4,0),
=(0,2,-4),
∴
,解得
∴
=(-
,2,1)
平面PAC的法向量取为
=
=(-2
,2,0)
∴cos<
,
>=
=
=
=
∴二面角A-PC-D的余弦值为
.
又tan∠ABD=
| AD |
| AB |
| ||
| 3 |
| BC |
| AB |
| 3 |
∴∠ABD=30,°∠BAC=60°
∴∠AEB=90°,即BD⊥AC
又PA∩AC=A,
∴BD⊥平面PAC.
(Ⅱ)过E作EF⊥PC,垂足为F,连接DF,
∵DE⊥平面PAC,EF是DF在平面PAC上的射影,由三垂线定理知PC⊥DF,
∴∠EFD为二面角A-PC-D的平面角.
又∠DAC=90°-∠BAC=30°
∴DE=ADsin∠DAC=1,AE=ABsin∠ABE=
| 3 |
又AC=4
| 3 |
∴EC=3
| 3 |
由Rt△EFC∽Rt△PAC得EF=
| PA•EC |
| PC |
3
| ||
| 2 |
在Rt△EFD中,tan∠EFD=
| DE |
| EF |
2
| ||
| 9 |
∴cos∠EFD=
| 9 |
| 93 |
| 93 |
∴二面角A-PC-D的余弦值为
| 9 |
| 93 |
| 93 |
解法二:(Ⅰ)如图,建立坐标系,则A(0,0,0),B(2
| 3 |
| 3 |
∴
| AP |
| AC |
| 3 |
| BD |
| 3 |
∴
| BD |
| AP |
| BD |
| AC |
∴BD⊥AP,BD⊥AC,又PA∩AC=A
∴BD⊥平面PAC.
(Ⅱ)设平面PCD的法向量为
| n |

则
| CD |
| n |
| PD |
| n |
又
| CD |
| 3 |
| PD |
∴
|
|
∴
| n |
| 4 |
| 3 |
| 3 |
平面PAC的法向量取为
| m |
| BD |
| 3 |
∴cos<
| n |
| BD |
| ||||
|
|
| 12 | ||||
|
| 9 | ||
|
| 9 |
| 93 |
| 93 |
∴二面角A-PC-D的余弦值为
| 9 |
| 93 |
| 93 |


练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目