题目内容
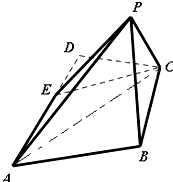
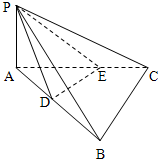
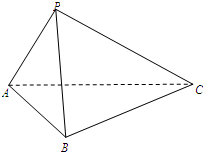
如图,在平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
(1)求二面角E-AB-D的大小;
(2)求四面体ABDE的表面积.
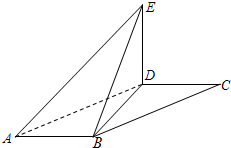
(1)求二面角E-AB-D的大小;
(2)求四面体ABDE的表面积.

(1)在△EBD中,
∵∠DAB=60°,AB=2,AD=4,
∴BD=
=2
.
∴AB2+BD2=AD2,∴AB⊥BD.
∵平面EBD⊥平面ABD,∴AB⊥平面BDE,∴AB⊥BE.
∴∠DBE即为二面角E-AB-D的平面角.
又∵CD⊥BD,∴ED⊥BD,而BD=2
,
DE=DC=AB=2,
∴在Rt△BDE中,cos∠DBE=
=
,
∴∠DBE=30°.
(2)由(1)知:AB⊥BD,
∴S△ABD=
AB•BD=2
.
又∵S△BDC=S△ABD=2
,而△EBD即为△BDC,
∴S△BDE=2
.
又∵AB⊥BE,BE=BC=AD=4,∴S△ABE=
AB•BE=4.
又DE⊥AD,∴S△ADE=
AD•DE=4.
故四面体ABDE的表面积为8+4
.
∵∠DAB=60°,AB=2,AD=4,
∴BD=
| AB2+AD2-2AB•ADcos∠DAB |
| 3 |
∴AB2+BD2=AD2,∴AB⊥BD.
∵平面EBD⊥平面ABD,∴AB⊥平面BDE,∴AB⊥BE.
∴∠DBE即为二面角E-AB-D的平面角.
又∵CD⊥BD,∴ED⊥BD,而BD=2
| 3 |
DE=DC=AB=2,
∴在Rt△BDE中,cos∠DBE=
| BD |
| BE |
| ||
| 2 |
∴∠DBE=30°.
(2)由(1)知:AB⊥BD,
∴S△ABD=
| 1 |
| 2 |
| 3 |
又∵S△BDC=S△ABD=2
| 3 |
∴S△BDE=2
| 3 |
又∵AB⊥BE,BE=BC=AD=4,∴S△ABE=
| 1 |
| 2 |
又DE⊥AD,∴S△ADE=
| 1 |
| 2 |
故四面体ABDE的表面积为8+4
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目