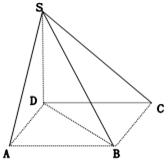
题目内容
如图，已知等边三角形ABC与正方形ABDE有一公共边AB，二面角C-AB-D的余弦值为
，M是AC的中点，则EM，DE所成角的余弦值等于______．
| ||
| 3 |
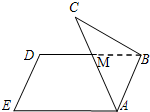
连结CD、CE，取AB的中点H，
设点C在平面ABDE内的射影为O，连结CO、OH、CH
∵CH是等边三角形ABC的中线，∴CH⊥AB
∵CO⊥平面ABDE，得OH是CH在平面ABDE内的射影
∴OH⊥AB，得∠OHC就是二面角C-AB-D的平面角
设AB=2，则等边△ABC中，CH=
AB=
Rt△COH中，cos∠OHC=
=
，可得OH=
CH=1，
由此可得点O是正方开ABDE的中心，可得四棱锥C-ABDE是所有棱长均为2的正四棱锥
等边△ACE中，
=
（
+
）且|
|=
∴
•
=
•（
+
）=
•
+
•
∵∠DEA=90°，得
•
=0；∠DEC=60°，得
•
=|
|•|
|cos60°=2
∴
•
=
×0+
×2=1
可得cos＜
，
＞=
=
=
由此结合两条直线所成角的定义，可得直线EM、DE所成角的余弦值等于
．
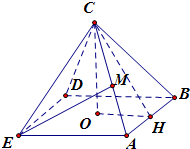
设点C在平面ABDE内的射影为O，连结CO、OH、CH
∵CH是等边三角形ABC的中线，∴CH⊥AB
∵CO⊥平面ABDE，得OH是CH在平面ABDE内的射影
∴OH⊥AB，得∠OHC就是二面角C-AB-D的平面角
设AB=2，则等边△ABC中，CH=
| ||
| 2 |
| 3 |
Rt△COH中，cos∠OHC=
| OH |
| CH |
| ||
| 3 |
| ||
| 3 |
由此可得点O是正方开ABDE的中心，可得四棱锥C-ABDE是所有棱长均为2的正四棱锥
等边△ACE中，
| EM |
| 1 |
| 2 |
| EA |
| EC |
| EM |
| 3 |
∴
| ED |
| EM |
| 1 |
| 2 |
| ED |
| EA |
| EC |
| 1 |
| 2 |
| ED |
| EA |
| 1 |
| 2 |
| ED |
| EC |
∵∠DEA=90°，得
| ED |
| EA |
| ED |
| EC |
| ED |
| EC |
∴
| ED |
| EM |
| 1 |
| 2 |
| 1 |
| 2 |
可得cos＜
| ED |
| EM |
| ||||
|
|
| 1 | ||
2×
|
| ||
| 6 |
由此结合两条直线所成角的定义，可得直线EM、DE所成角的余弦值等于
| ||
| 6 |
练习册系列答案
阅读快车系列答案
相关题目
