题目内容
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在矩形ABCD的边BC上移动.
(Ⅰ)证明:无论点E在边BC的何处,都有PE⊥AF;
(Ⅱ)当CE等于何值时,二面角P-DE-A的大小为45°.
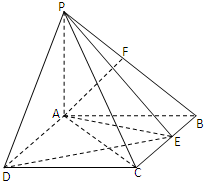
(Ⅰ)证明:无论点E在边BC的何处,都有PE⊥AF;
(Ⅱ)当CE等于何值时,二面角P-DE-A的大小为45°.

(I)证明:∵PA⊥平面ABCD,BE?平面ABCD,
∴EB⊥PA,
又∵EB⊥AB,AB∩AP=A,AB,AP?平面PAB,
∴EB⊥平面PAB,
又∵AF?平面PAB,∴AF⊥BE,
又∵PA=AB=1,点F是PB的中点,
∴AF⊥平面PBE.
∵PE?平面PBE,
∴AF⊥PE.
(II)过A作AG⊥DG于G,连PG,
∵DE⊥PA,∴DE⊥平面PAG,则∠PAG是二面角P-DE-A的平面角,
∴∠PGA=45°
∵PD与平面ABCD所成角是30°,
∴∠PDA=30°,
∴AD=
,PA=AB=1.
∴AG=1,DG=
,
设BE=x,则GE=x,CE=
-x,
在Rt△DCE中,(
+x)2=(
-x)2+12,
得BE=x=
-
.
故CE=
.
∴EB⊥PA,
又∵EB⊥AB,AB∩AP=A,AB,AP?平面PAB,
∴EB⊥平面PAB,
又∵AF?平面PAB,∴AF⊥BE,
又∵PA=AB=1,点F是PB的中点,
∴AF⊥平面PBE.
∵PE?平面PBE,
∴AF⊥PE.
(II)过A作AG⊥DG于G,连PG,
∵DE⊥PA,∴DE⊥平面PAG,则∠PAG是二面角P-DE-A的平面角,
∴∠PGA=45°
∵PD与平面ABCD所成角是30°,
∴∠PDA=30°,
∴AD=
| 3 |
∴AG=1,DG=
| 2 |
设BE=x,则GE=x,CE=
| 3 |
在Rt△DCE中,(
| 2 |
| 3 |
得BE=x=
| 3 |
| 2 |
故CE=
| 2 |

练习册系列答案
相关题目