题目内容
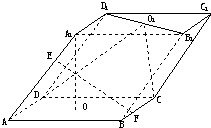
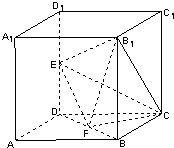
如图所示,在正方体ABCD-A1B1C1D1中,E为DD1上的点、F为DB的中点.
(Ⅰ)求直线B1F与平面CDD1C1所成角的正弦值;
(Ⅱ)若直线EF∥平面ABC1D1,试确定点E的位置.
(Ⅰ)求直线B1F与平面CDD1C1所成角的正弦值;
(Ⅱ)若直线EF∥平面ABC1D1,试确定点E的位置.

(Ⅰ)∵平面ABB1A1∥平面CDD1C1
∴直线B1F与平面CDD1C1所成角等于直线FB1与平面ABB1A1所成的角(2分)
取AB中点P,连接FP和B1P
由已知可得FP⊥AB,FP⊥BB1,故FP⊥平面ABB1A1
∴B1F与平面ABB1A1所成的角即为∠FB1P(4分)
在Rt△FPB1中,sin∠FB1P=
=
即B1F与平面CDD1C1所成角的正弦值为
.(6分)
(Ⅱ)连接BD1,则平面BDD1B1过EF与平面ABC1D1交于BD1
由EF∥平面ABC1D1可得EF∥BD1
又因为F为DB的中点
故得E也必须为DD1的中点.(12分)
∴直线B1F与平面CDD1C1所成角等于直线FB1与平面ABB1A1所成的角(2分)
取AB中点P,连接FP和B1P
由已知可得FP⊥AB,FP⊥BB1,故FP⊥平面ABB1A1
∴B1F与平面ABB1A1所成的角即为∠FB1P(4分)
在Rt△FPB1中,sin∠FB1P=
| FP |
| FB1 |
| ||
| 6 |
即B1F与平面CDD1C1所成角的正弦值为
| ||
| 6 |
(Ⅱ)连接BD1,则平面BDD1B1过EF与平面ABC1D1交于BD1
由EF∥平面ABC1D1可得EF∥BD1
又因为F为DB的中点
故得E也必须为DD1的中点.(12分)

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目