题目内容
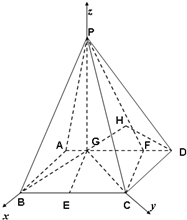
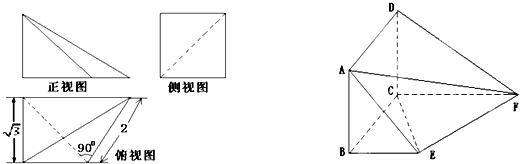
如图多面体,它的正视图为直角三角形,侧视图为矩形,俯视图为直角梯形(尺寸如图所示).
(Ⅰ)求证:AE∥平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为60°?
(Ⅰ)求证:AE∥平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为60°?

(Ⅰ)证明:由三视图可知:△ABE与△DCF皆为直角三角形,且AB⊥BE,DC⊥CF,
侧面矩形ABCD⊥底面直角梯形BEFC,且BC=
,EF=2,∠CEF=90°.
由以上可得:AB∥CD,BE∥CF.
又AB?平面DCF,DC?平面DCF,∴AB∥平面DCF;
同理可证BE∥平面DCF.
又AB∩BE=B,∴平面ABE∥平面DCF.
∴AE∥平面DCF.
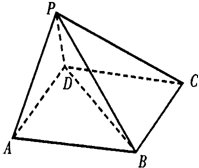
(Ⅱ)如图所示:
当AB=DC=6时,二面角A-EF-C的大小为60°.下面给出证明:
过点E作EM⊥CF,垂足为M,则EM∥BC,又BE∥CM,
∴四边形BCME为矩形,∴EM=
.
在Rt△EFM中,sin∠EFM=
=
,∴∠EFM=60°.
∴∠FEM=30°.
∵∠FEC=90°,∴∠CEM=60°,FE⊥CE.
在Rt△CEM中,CE=
=2
.
∵DC⊥BC,平面ABCD⊥平面BCFE,
∴DC⊥平面BCFE,∴DC⊥EF.
又∵DC∩CE=C,∴FE⊥平面DCE,∴FE⊥DE,
∴∠DCE是二面角A-EF-C的平面角,其大小为60°.
在Rt△DCE中,DC=CEtan60°=6=AB.
故当AB的长6时,二面角A-EF-C的大小为60°.
侧面矩形ABCD⊥底面直角梯形BEFC,且BC=
| 3 |
由以上可得:AB∥CD,BE∥CF.
又AB?平面DCF,DC?平面DCF,∴AB∥平面DCF;
同理可证BE∥平面DCF.

又AB∩BE=B,∴平面ABE∥平面DCF.
∴AE∥平面DCF.
(Ⅱ)如图所示:
当AB=DC=6时,二面角A-EF-C的大小为60°.下面给出证明:
过点E作EM⊥CF,垂足为M,则EM∥BC,又BE∥CM,
∴四边形BCME为矩形,∴EM=
| 3 |
在Rt△EFM中,sin∠EFM=
| EM |
| EF |
| ||
| 2 |
∴∠FEM=30°.
∵∠FEC=90°,∴∠CEM=60°,FE⊥CE.
在Rt△CEM中,CE=
| ME |
| cos60° |
| 3 |
∵DC⊥BC,平面ABCD⊥平面BCFE,
∴DC⊥平面BCFE,∴DC⊥EF.
又∵DC∩CE=C,∴FE⊥平面DCE,∴FE⊥DE,
∴∠DCE是二面角A-EF-C的平面角,其大小为60°.
在Rt△DCE中,DC=CEtan60°=6=AB.
故当AB的长6时,二面角A-EF-C的大小为60°.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目