Question

【题目】（12分）已知椭圆的离心率为，椭圆C的长轴长为4．

（1）求椭圆C的方程；

（2）已知直线与椭圆C交于A，B两点，是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O？若存在，求出k的值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）存在实数使得以线段AB为直径的圆恰好经过坐标原点O．

【解析】

试题本题主要考查椭圆的标准方程及其几何性质、直线与椭圆的位置关系等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力．第一问，利用椭圆的离心率和长轴长列出方程，解出a和c的值，再利用计算b的值，从而得到椭圆的标准方程；第二问，将直线与椭圆联立，消参，利用韦达定理，得到、，由于以线段AB为直径的圆恰好经过坐标原点O，所以，即，代入和，解出k的值．

试题解析：（1）设椭圆的焦半距为c，则由题设，得，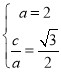

解得，所以，

故所求椭圆C的方程为．

（2）存在实数k使得以线段AB为直径的圆恰好经过坐标原点O．

理由如下：

设点，，

将直线的方程代入，

并整理，得．（*）

则，．

因为以线段AB为直径的圆恰好经过坐标原点O，

所以，即．

又，

于是，解得，

经检验知：此时（*）式的Δ＞0，符合题意．

所以当时，以线段AB为直径的圆恰好经过坐标原点O．