题目内容
已知函数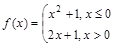 ,若
,若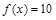 ,则
,则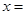 .
.
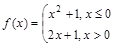 ,若
,若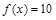 ,则
,则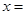 .
.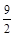 或
或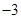
试题分析:根据题意,那么要使得f(x)=10,则需要对于x属于哪一段的变量进行讨论。
当
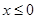 时,则
时,则 (舍)
(舍)当
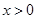 时,则
时,则 ,综上可知满足题意的x的取值有两个,且为
,综上可知满足题意的x的取值有两个,且为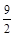 或
或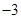 。
。点评:解决该试题的关键是理解,函数值的求解,需要对于x进行分类讨论,来确定解集。同时要熟练一元二次方程的求解运用,属于基础题。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
题目内容
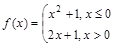 ,若
,若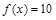 ,则
,则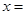 .
.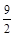 或
或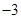
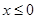 时,则
时,则 (舍)
(舍)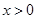 时,则
时,则 ,综上可知满足题意的x的取值有两个,且为
,综上可知满足题意的x的取值有两个,且为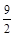 或
或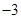 。
。
 口算能手系列答案
口算能手系列答案