题目内容
(本小题满分14分)
若函数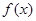 对任意的实数
对任意的实数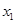 ,
,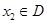 ,均有
,均有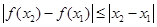 ,则称函数
,则称函数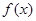 是区间
是区间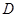 上的“平缓函数”.
上的“平缓函数”.
(1) 判断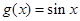 和
和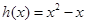 是不是实数集R上的“平缓函数”,并说明理由;
是不是实数集R上的“平缓函数”,并说明理由;
(2) 若数列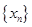 对所有的正整数
对所有的正整数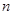 都有
都有 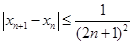 ,设
,设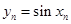 ,
,
求证: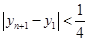 .
.
若函数
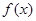 对任意的实数
对任意的实数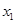 ,
,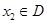 ,均有
,均有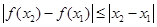 ,则称函数
,则称函数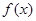 是区间
是区间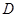 上的“平缓函数”.
上的“平缓函数”. (1) 判断
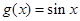 和
和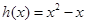 是不是实数集R上的“平缓函数”,并说明理由;
是不是实数集R上的“平缓函数”,并说明理由;(2) 若数列
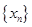 对所有的正整数
对所有的正整数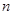 都有
都有 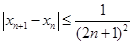 ,设
,设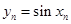 ,
, 求证:
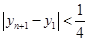 .
.(1)不是,理由见解析 (2)见解析
(本小题主要考查函数、绝对值不等式等基础知识,考查函数与方程、分类与整合、化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力、创新意识)
(1)解: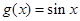 是R上的“平缓函数”,但
是R上的“平缓函数”,但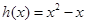 不是区间R的“平缓函数”;
不是区间R的“平缓函数”;
设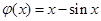 ,则
,则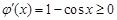 ,则
,则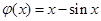 是实数集R上的增函数,
是实数集R上的增函数,
不妨设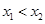 ,则
,则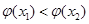 ,即
,即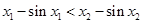 ,
,
则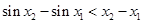 . ① …………… 1分
. ① …………… 1分
又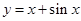 也是R上的增函数,则
也是R上的增函数,则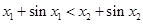 ,
,
即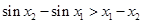 , ② ………… 2分
, ② ………… 2分
由①、②得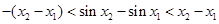 .
.
因此,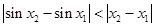 ,对
,对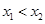 都成立. ……… 3分
都成立. ……… 3分
当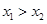 时,同理有
时,同理有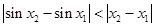 成立
成立
又当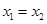 时,不等式
时,不等式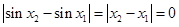 ,
,
故对任意的实数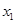 ,
,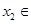 R,均有
R,均有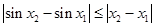 .
.
因此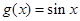 是R上的“平缓函数”. ………… 5分
是R上的“平缓函数”. ………… 5分
由于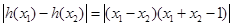 ………… 6分
………… 6分
取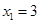 ,
,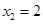 ,则
,则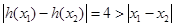 , ………… 7分
, ………… 7分
因此,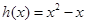 不是区间R的“平缓函数”. ………… 8分
不是区间R的“平缓函数”. ………… 8分
(2)证明:由(1)得: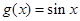 是R上的“平缓函数”,
是R上的“平缓函数”,
则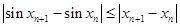 , 所以
, 所以 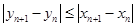 . …………… 9分
. …………… 9分
而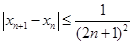 ,
,
∴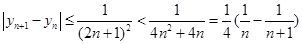 . …………… 10分
. …………… 10分
∵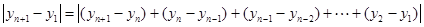 ,……… 11分
,……… 11分
∴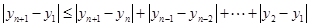 . …………… 12分
. …………… 12分
∴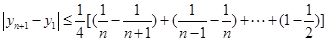
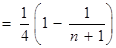 ………… 13分
………… 13分
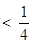 . ………… 14分
. ………… 14分
(1)解:
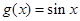 是R上的“平缓函数”,但
是R上的“平缓函数”,但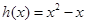 不是区间R的“平缓函数”;
不是区间R的“平缓函数”;设
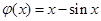 ,则
,则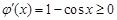 ,则
,则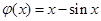 是实数集R上的增函数,
是实数集R上的增函数,不妨设
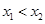 ,则
,则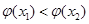 ,即
,即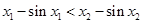 ,
, 则
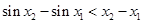 . ① …………… 1分
. ① …………… 1分又
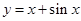 也是R上的增函数,则
也是R上的增函数,则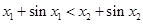 ,
,即
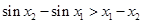 , ② ………… 2分
, ② ………… 2分由①、②得
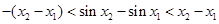 .
. 因此,
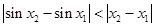 ,对
,对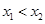 都成立. ……… 3分
都成立. ……… 3分当
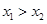 时,同理有
时,同理有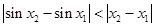 成立
成立又当
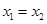 时,不等式
时,不等式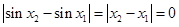 ,
,故对任意的实数
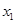 ,
,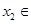 R,均有
R,均有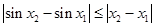 .
.因此
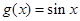 是R上的“平缓函数”. ………… 5分
是R上的“平缓函数”. ………… 5分由于
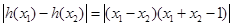 ………… 6分
………… 6分取
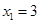 ,
,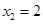 ,则
,则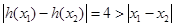 , ………… 7分
, ………… 7分因此,
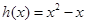 不是区间R的“平缓函数”. ………… 8分
不是区间R的“平缓函数”. ………… 8分(2)证明:由(1)得:
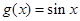 是R上的“平缓函数”,
是R上的“平缓函数”,则
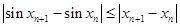 , 所以
, 所以 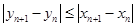 . …………… 9分
. …………… 9分而
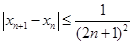 ,
,∴
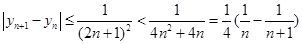 . …………… 10分
. …………… 10分∵
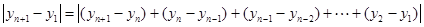 ,……… 11分
,……… 11分∴
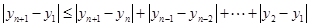 . …………… 12分
. …………… 12分∴
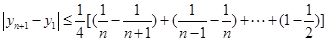
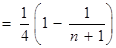 ………… 13分
………… 13分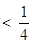 . ………… 14分
. ………… 14分
练习册系列答案
相关题目
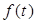 (元)与时间
(元)与时间 (天)的函数关系近似满足
(天)的函数关系近似满足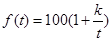 (
(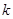 为正的常数),日销售量
为正的常数),日销售量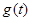 (件)与时间
(件)与时间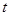 (天)的函数关系近似满足
(天)的函数关系近似满足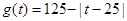 ,且第25天的销售金额为13000元.
,且第25天的销售金额为13000元.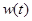 关于时间
关于时间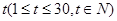 的函数关系式,并求前半个月销售金额
的函数关系式,并求前半个月销售金额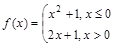 ,若
,若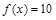 ,则
,则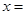 .
.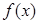 为
为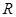 上的减函数,则满足
上的减函数,则满足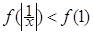 的实数
的实数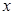 的取值范围是( )
的取值范围是( )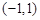
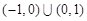
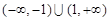
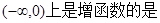 ( )
( )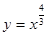
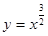
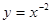
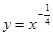
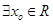 ,使
,使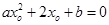 成立,则
成立,则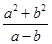 的最小值为( )
的最小值为( )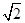
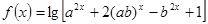
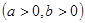 ,求使
,求使 成立的
成立的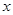 的取值范围。(10分)
的取值范围。(10分)