题目内容
(1)若不等式
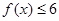 的解集为
的解集为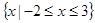 ,求实数
,求实数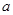 的值;
的值;(2)在(1)的条件下,若存在实数
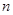 使
使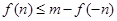 成立,求实数m的取值范围。
成立,求实数m的取值范围。(1)1(2)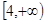
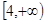
19.试题分析:(1)由
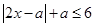 得,
得,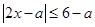
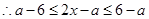 ,即
,即 。
。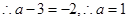 .......................................4分
.......................................4分(2)由(1)知
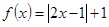 ,令
,令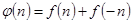 ,
,则
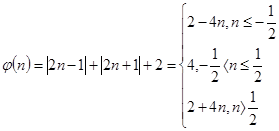 .........................7分
.........................7分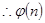 的最小值为4,故实数m的取值范围是
的最小值为4,故实数m的取值范围是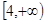 .................10分
.................10分点评:解决该是的关键是理解一元二次不等式的解集是不等式成立的充要条件。同时对于含有绝对值的函数,利用分段函数的思想得到其最值,这也是在选修部分中常考的知识点之一,属于基础题。

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
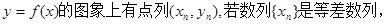 数列{
数列{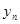 }是等比数列,则函数
}是等比数列,则函数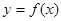 的解析式可能为( )
的解析式可能为( )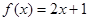
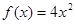
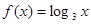
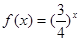
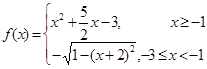 ,则函数
,则函数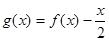 的零点个数为
的零点个数为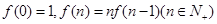 ,则
,则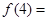
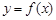 满足:①
满足:①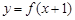 是偶函数;②在区间
是偶函数;②在区间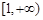 上是增函数.若
上是增函数.若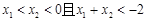 ,则
,则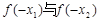 的大小关系是( )
的大小关系是( )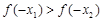
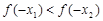
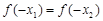
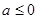 ,函数
,函数 .
. 在
在 上的奇偶性;
上的奇偶性;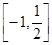 上的最大值。
上的最大值。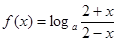 (
(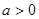 且
且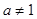 ).
).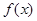 的定义域;
的定义域;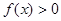 的
的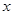 取值范围.
取值范围.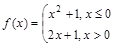 ,若
,若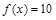 ,则
,则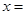 .
.