题目内容
1.已知中心均在原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1、e2,则e1e2的取值范围为( )| A. | $({\frac{1}{3},+∞})$ | B. | $({\frac{2}{3},1})$ | C. | (2,+∞) | D. | $({\frac{3}{2},+∞})$ |
分析 设椭圆和双曲线的半焦距为c,|PF1|=m,|PF2|=n,(m>n),由条件可得m=10,n=2c,再由椭圆和双曲线的定义可得a1=5+c,a2=5-c,(c<5),运用三角形的三边关系求得c的范围,再由离心率公式,计算即可得到所求范围.
解答 解:设椭圆和双曲线的半焦距为c,|PF1|=m,|PF2|=n,(m>n),
由于△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,
即有m=10,n=2c,
由椭圆的定义可得m+n=2a1,
由双曲线的定义可得m-n=2a2,
即有a1=5+c,a2=5-c,(c<5),
再由三角形的两边之和大于第三边,可得2c+2c>10,
可得c>$\frac{5}{2}$,即有$\frac{5}{2}$<c<5.
由离心率公式可得e1•e2=$\frac{c}{{a}_{1}}•\frac{c}{{a}_{2}}$=$\frac{{c}^{2}}{25-{c}^{2}}$=$\frac{1}{\frac{25}{{c}^{2}}-1}$,
由于1<$\frac{25}{{c}^{2}}$<4,则有$\frac{1}{\frac{25}{{c}^{2}}-1}$>$\frac{1}{3}$.
则e1•e2 的取值范围为($\frac{1}{3}$,+∞).
故选:A.
点评 本题考查椭圆和双曲线的定义和性质,考查离心率的求法,考查三角形的三边关系,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
11.已知直线l1:y=kx+1和直线l2:y=mx+m,则“k=m”是“l1∥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.如图是某算法的程序框图,若程序运行后输出的结果是27,则判断框①处应填入的条件是( )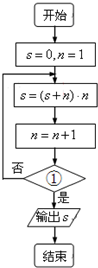

| A. | n>2 | B. | n>3 | C. | n>4 | D. | n>5 |
11.若曲线C1:x2+y2-2x=0与曲线C2:y(y-mx-m)=0有四个不同的交点,则实数m的取值范围是( )
| A. | (-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) | B. | (-∞,-$\frac{\sqrt{3}}{3}$)∪($\frac{\sqrt{3}}{3}$,+∞) | C. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | D. | (-$\frac{\sqrt{3}}{3}$,0)∪(0,$\frac{\sqrt{3}}{3}$) |