题目内容
13.方程ρ=$\frac{1}{1-cosθ+sinθ}$表示的曲线是双曲线.分析 把极坐标方程ρ=$\frac{1}{1-cosθ+sinθ}$化为直角坐标方程,根据直角坐标方程判断该曲线表示的什么图形.
解答 解:极坐标方程ρ=$\frac{1}{1-cosθ+sinθ}$可化为,
ρ-ρcosθ+ρsinθ=1,
即$\sqrt{{x}^{2}{+y}^{2}}$-x+y=1,
整理,得1+2x-2y-2xy=0;
即xy-x+y=$\frac{1}{2}$,
∴(x+1)(y-1)=-$\frac{1}{2}$;
令x'=x+1,y'=y-1,
曲线方程可化为x'y'=-$\frac{1}{2}$,
它表示反比例函数,是双曲线.
故答案为:双曲线.
点评 本题考查了极坐标方程化为直角坐标系方程的应用问题,也考查了坐标变换的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设x,y满足不等式组$\left\{{\begin{array}{l}{x+y-6≤0}\\{2x-y-1≤0}\\{3x-y-2≥0}\end{array}}\right.$,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
| A. | [-1,2] | B. | [-2,1] | C. | [-3,-2] | D. | [-3,1] |
1.已知中心均在原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1、e2,则e1e2的取值范围为( )
| A. | $({\frac{1}{3},+∞})$ | B. | $({\frac{2}{3},1})$ | C. | (2,+∞) | D. | $({\frac{3}{2},+∞})$ |
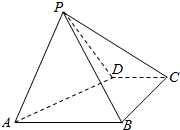 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD 是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD 是以AD为底的等腰三角形.